Deep Neural Network는 Deep 이름표가 붙지 않는 전통적인 머신러닝 기법들의 총 집합체라고 볼 수 있습니다. 이번 포스팅에서는 Deep Neural Network의 구조와 구성요소를 살펴봅니다.
살펴볼 내용들
- Deep Neural Network란
- Deep Neural Network의 구성요소
- Deep Neural Network의 구조형성 방법
Deep Neural Network란
Supervised Deep Learning - Definition
데이터 비선형성이 심할 경우, 데이터를 분류하는 문제를 풀기 어렵다
전통적인 머신러닝 접근법
- 이미지에 Convolution Filter 활용
- 선형 형태에 가깝게 변형
- 클래스 구분
전통적인 머신러닝 접근법의 문제: Overfitting
Kernelization 활용
- convolution filter 등으로 feature를 뽑았음에도 비선형성이 복잡하게 남아있는 경우, Kernel 사용
- 기존의 feature에 가상의 feature 고려
- 비선형성 feature를 선형으로 변환
- 머신러닝 기법으로 분류
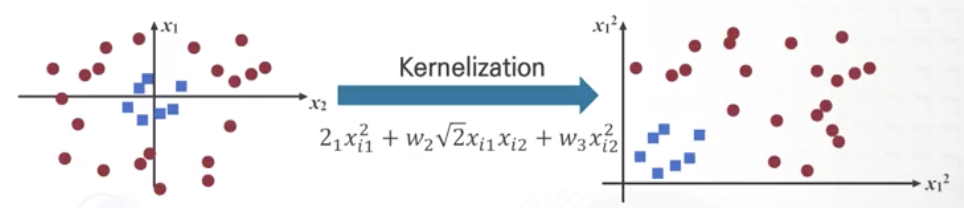
- 비선형성 해결 위해 모델을 키우고 복잡한 Kernel 적용
- Overfitting 문제도 비례하여 증가
“비선형성과 과적합 문제가 전통적인 머신러닝 접근법의 근본적인 문제점”
딥러닝은 복잡한 비선형성을 어떻게 풀까?
수많은 간단한 비선형성을 융합하는 형태로 해결
- 간단한 비선형성을 반복적으로 현재 데이터에 적용
- 더 복잡한 비선형성을 표현할 수 있게 구현

딥러닝은 과적합 문제를 어떻게 풀 수 있을까?
전통적 머신러닝 접근법의 과적합 이슈
- Kernelization 단계에서 더 복잡한 Kernel 사용
- 파라미터 증가
- Overfitting 문제 발생
딥러닝에서는 데이터를 많이 많이 사용함으로써 문제 해결
- 데이터가 충분히 많음 = iid 성립
- iid = identically and independently dependent
- 학습데이터와 테스트데이터가 어느 정도 동일한 샘플 분포, 데이터 분포를 형성함
- 학습데이터가 충분히 크다 = 테스트 데이터를 학습 데이터가 충분히 표현하고 있다
- 학습데이터에 대해 overfitting이 발생하더라도, 학습데이터가 크기 때문에 overfitting된 결과가 테스트에 대해서도 높은 성능을 보이도록 하는 것
- 테스트 데이터에서도 잘 동작하면 더 이상 Overfitting이 아니다!
- 항상 딥러닝에서 데이터 사이즈가 중요하다는 것이 강조되는 이유
딥러닝 vs. 전통 머신러닝 활용 방향성
전통적 머신러닝 : 모든 데이터 중 일부를 샘플링하여 활용
딥러닝 : 모든 데이터를 고려해서 학습하는 방법을 채택
Deep Neural Network
- Convolution Neural Network
- 이미지 분류를 위해서 활용되는 모델
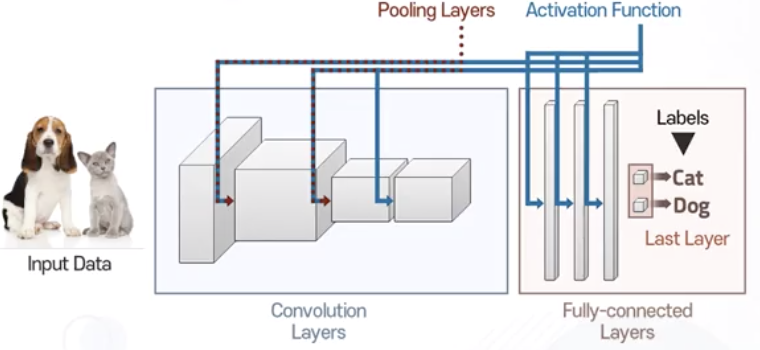
- 특정 이미지 입력
- Convolution layer 통과
- Fully-connected layer 통과
- 예측 결과값 출력
DNN : Convolution Layer
- 여러 개의 레이어로 구성
- 각각의 레이어는 서로 다른 학습과정과 테스트 과정을 거침
- 각 레이어 사이에는 Pooling layer가 존재함
DNN : Fully-conneected Layer
- 여러 개의 Fully-connected layer들로 구성
- 첫 번째 Fully connected layer 입력받음
- 입력값 변형
- 변형된 입력값을 두 번째 Fully-connected layer로 입력
- 입력값 변형
- …
- 마지막 Fully-connected layer (Last Layer) 입력
- Last Layer = 최종적으로 입력받은 feature를 기반으로 우리가 원하는 라벨을 출력해주는 제일 마지막 레이어
DNN : Activation Function
- 각각의 convolution layer와 fully-connected layer의 뒷단에 배치
- 비선형성을 표현하기 위한 존재 (추후 자세히 살펴봄)
Deep Neural Network의 구성요소
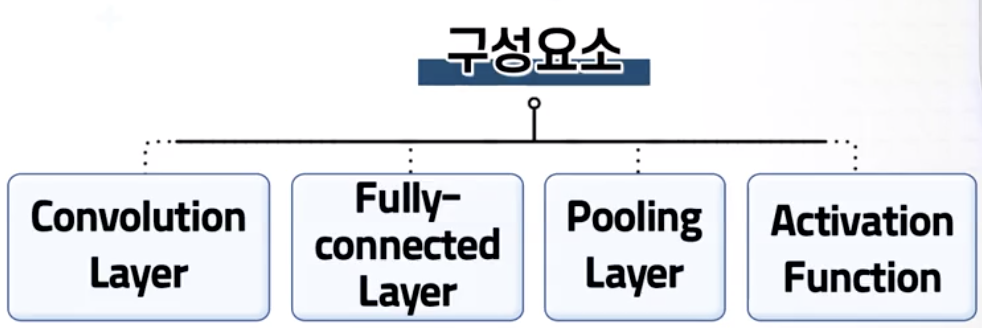
Convolution Layer
Layer for Feature Engineering
- Convolution Filter의 종류
- Gaussian filter (평균)
- Sharpen convolution (경계선 강조)
- Laplacian
- Laplacian of Gaussian filter (Gaussian + Laplacian)
Filter Banks
- 여러 개의 Filter를 실제 이미지에 적용한 결과 모음
- 결과값들을 그대로 머신러닝 모델의 입력값으로 활용
- 이미지 입력 시 여러 필터들이 적용된 여러 결과값을 출력

그 다음에 있는 Convolution Layer는?
- 이전 Convolution Layer에서 출력된 필터 결과값들을 기반으로 다시 필터들을 적용하는 구조
Tranditional Filters vs. Convolutional Layers
- 중요한 차이 = “어떤 값이 정답인가?”
- 출력 목표값이 필요하지만 현재로선 모르는 상황
- Hidden Feature 또는 Latent Feature
- 구조 : 반복적 구성
- 입력값 = 일반 이미지 또는 다른 convolution layer의 필터 결과
- 기존 convolution 필터와 딥러닝의 convolution filter layer 작동원리는 크게 다르지 않음

실제 Convolution Layer 필터 학습결과 예시
- ZFNet 이라는 논문 내용 일부
- “각 레이어에서 실제로 어떤 필터들이 학습되었는지 알아낼 수 있으며, 이를 시각화할 수 있다.”
- Gabor filter 등 익숙한 필터들이 Deep Neural Network 내부에서 학습되는 모습을 확인할 수 있음
- 뒤에 배치된 convolution layer일수록 좀 더 복잡한 형태의 필터들로 구성되고 있음을 확인할 수 있음

Pooling Layer
어떤 이미지 또는 필터의 결과값의 해상도를 낮춰주는 역할
- 예) 입력된 이미지 데이터가 $100*100$ 해상도의 이미지일 경우
- 필터 갯수가 1000개이면, $1001001000$ 크기의 결과값!
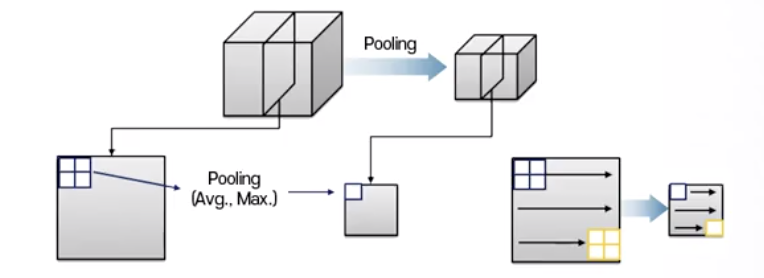
- Pooling layer에 입력된 어떤 feature의 결과값들 중 최대값 1개를 선택
- 상대적으로 작은 Resolution 이미지의 저해상도 이미지 한 개 값으로 배정
- 4개의 픽셀이 1개의 픽셀로 바뀐 효과
- 기존 입력된 이미지보다 해상도가 훨씬 낮은 feature 결과
- 입력된 이미지 크기보다 훨씬 작은 필터 결과값을 얻음
- 비선형성 개선시키는 효과
- 계산 효율성도 훨씬 높일 수 있음
Pooling layer는 convolution layer 중간 중간에 위치하여, 각각의 convolution layer가 거쳤을 때 얻을 필터 결과값의 해상도를 줄여주는 역할을 수행한다.
Fully-connected Layer (FC Layer)
Fully-connected layer는 가장 마지막 Last Layer를 제외하고는 linear regression 모델과 동일 역할을 수행함
Linear Regression vs. Fully connected layer
Linear Regression \(\hat{y_i}=\sum_{j=1}^dw_jx_{ij}\)
- 각각 서로 다른 $W$를 곱하고 그것의 합을 예측값으로 출력
- 한 개의 아웃풋
Fully connected layer
- 여러 개의 아웃풋 (128 ~ 2048개)
- 입력된 feature에 어떤 $W$를 곱하고, 그 $W$에 출력되는 값이 여러 개 있는 구조
- 즉, linear regressor가 여러 개 있는 것과 똑같은 구조
- 목표 : 원하는 prediction 결과와 최대한 비슷하게 출력
- Convolution Layer와 마찬가지로 목표값이 없음
- 목표값이 어떤 값인지 모르는 상황 = Hidden Feature 또는 Latent Feature
Linear Classification Model vs. Fully-connected Layer
| Linear Classification Model | Fully-connected Layer |
|---|---|
| 정해진 필터를 적용한 결과값이나 주어진 데이터를 그대로 활용하여 input | 수많은 convolution layer와 fully-connected layer를 통해서 여러 번 계산(정제)된 feature를 input |
Activation Function
- 간단한 비선형성을 구현하는 부분
- 인간의 뉴런에서 착안된 구성요소
- 인간 뉴런 = 0보다 작은 값은 무시 (전달하지 않음)
- Activation function 예
- 특정 threshold 이하의 값이면 0 출력
- 일정 이상이 나오는 경우, 특정 1 혹은 2의 값 출력
- activation function = 비선형성을 표현하는 간단한 함수
- 모든 레이어의 뒷단에 붙여준다
- 레이어가 한 단씩 끝날 때마다 반복된다
- 간단한 비선형 변환을 반복하여 매우 복잡한 비선형성을 해결한다
Kernel Trick vs. Activation Function
Kernel Trick
- 단점: 데이터 feature dimension이 커지면 커질수록 복잡도 증가
Activation Function
- 함수 형태를 고정한 뒤 그대로 반복 사용
- 속도가 더욱 빠름
- 구조가 단순함
Activation Function은 왜 레이어 뒷단마다 필요할까?
- 여러 개의 convolutoin filter / fully-connected layer를 아무리 쌓아도, 단 한 개의 convolution filter / fully-connected layer를 적용한 것과 동일한 결과가 나옴
- 크게 보면 convolution filter를 1회 적용한 결과와 같아짐
- Fully-connected layer의 경우 각 레이어가 linear regressor 역할을 수행하는 데, 결국 크게 보면 $Wx$를 계산해 모두 더할 뿐이므로 하나의 $Wx$와 크게 다르지 않게 됨
- Activation Function은 layer 간의 선형성(linearity)이 유지되지 않도록 각각의 layer 뒷단에 붙어주어야 함!
정리 요약
- 이미지 주어짐
- convolution layer 통과
- convolution layer 뒷단 activation function 작동
- pooling layer 통해 결과 이미지 해상도 축소
- 줄어든 filter 값에 대해 또 다른 convolution layer 적용
- 2-5 반복함
- 여러 개의 convolution layer로부터 최종적인 필터 결과값 출력 > Fully-connected layer에 입력
- 각각의 fully-connected layer는 앞서 배운 linear regressor와 동일 역할을 수행함
- 앞서 나왔던 필터의 결과값들을 조금씩 변경시켜 나감
- fully-connected layer 뒷단 activation function 작동
- (Last Layer) linear classification 모델과 동일하게 입력된 feature를 기반으로 카테고리 출력
Deep Neural Network 특징/장점
- convolution filter, function for non-linearity, linear regress, linear classification 모델 등이 모두 묶여 있는 모델
- 데이터에 어떤 추가적인 과정 없이 순수한 데이터로부터 우리가 원하는 모델을 만들어낼 수 있음
- convolution filter 설계할 필요 없이 데이터와 라벨만 주어지면 학습 가능
- 여 개의 non-linear activation function을 레이어 뒷단마다 배치하여 비선형성을 상당히 잘 표현
- 수많은 filter와 fully-connected layer가 갖는 수많은 파라미터들로, 아무리 데이터가 많아도 과적합 없이 트레이닝 데이터와 테스트 데이터 양쪽을 잘 표현할 수 있음
K-mooc, 딥러닝의 깊이 있는 이해를 위한 머신러닝, 중앙대학교 첨단영상대학원 영상학과 최종원 교수님
*그래프 이미지 출처: 강의자료