Non-linear Data 처리 방법

작성일 | In ,

우리가 현실에서 맞닥뜨리는 대부분의 데이터는 비선형 데이터에 속합니다. 그러나 선형 모델은 비선형 데이터를 표현할 수 없다는 근본적인 한계를 갖고 있는데요. 오늘은 살펴볼 내용은 다음과 같습니다.

  • 논리니어 데이터를 머신러닝 데이터로 활용하는 방법
  • 기존의 선형 모델을 변형하여 비선형 모델을 처리할 수 있는가

앞서 작성된 글:

살펴볼 내용들

  • Non-linear Data의 정의와 사용법
  • Non-linear Data를 위한 Feature 추출 과정
  • 이미지 데이터의 Feature 추출 과정
    • Bag-of-Word 방법론
    • 이미지에서 필터 기반 Feature 추출 방법을 상황에 맞게 적용하는 법

Non-linear Data의 정의 및 사용법

Non-linear Data

선형의 단순한 모델로 표현하지 못하는 데이터 = Non-linear Data

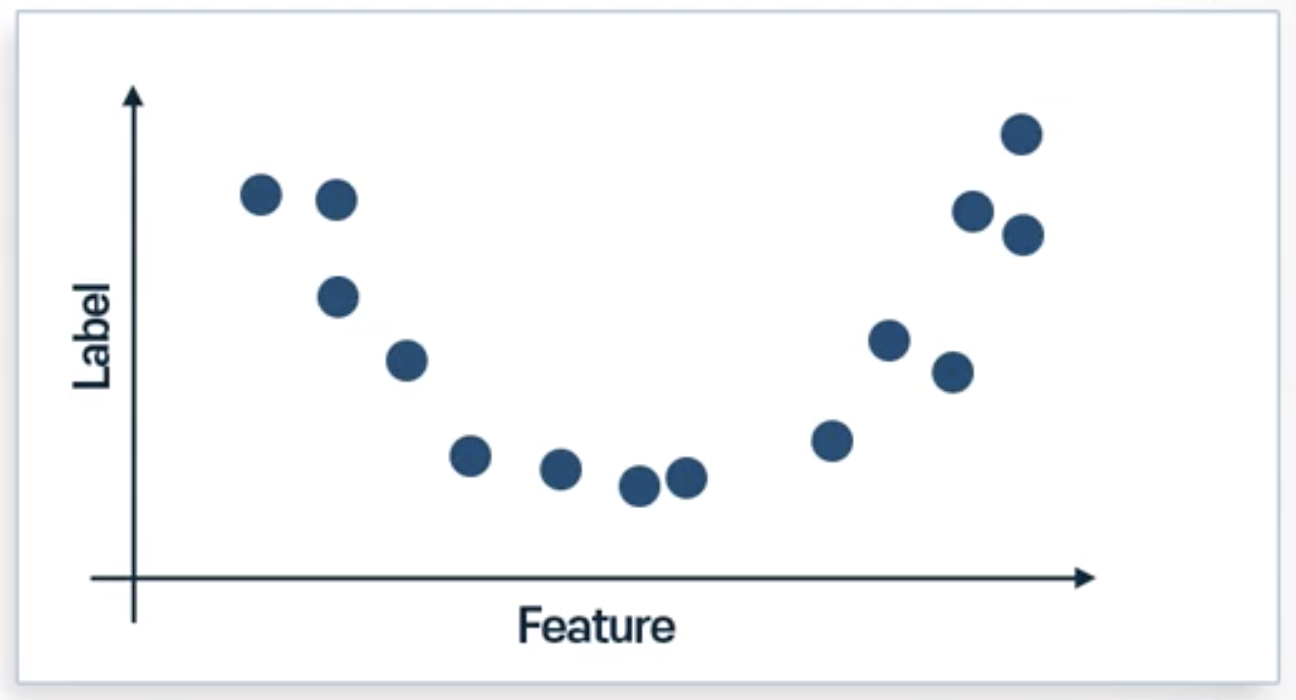
image-20210127120800383

  • Non-linear Data를 쉽게 표현할 수 있는 방법은?

Feature Engineering 모델

  • 입력된 feature를 한 번 바꿔주는 과정을 거침
    • 예) 그림이미지의 경우 피쳐를 픽셀 값으로 활용할 경우 비선형 데이터가 됨
    • 연관관계가 복잡하고 선형 표현이 어려우므로
    • 픽셀 값을 그대로 이용하지 않고, 추가로 알고리즘을 활용하여 전체 이미지를 표현함
      • 대표적인 Feature Engineering 방법으로는 Bag-of-Words가 있음

Kernel Trick (Feature Transform)

Feature Engineering Kernel Trick (Feature Transform)
현재 이미지나 데이터를 표현할 수 있는 피쳐 자체를 변형해서 다르게 추출 이미 추출된 피쳐를 한번 더 변형해서, 선형 모델로 비선형 데이터를 학습

Non-linear Data를 위한 Feature 추출 과정

Feature Engineering의 Bag-of-words

image-20210127121349690

  • 세 개의 데이터를 분류하기 위해 수많은 피쳐(pixel)가 입력됨
  • 입력된 피쳐들을 선형 분리시키는 작업 자체가 힘든 상태

Bag-of-words

  • 부분적인 특징들을 각각 한 개의 워드로 표현
  • 워드들의 조합으로 한 개의 이미지를 표현하는 방식

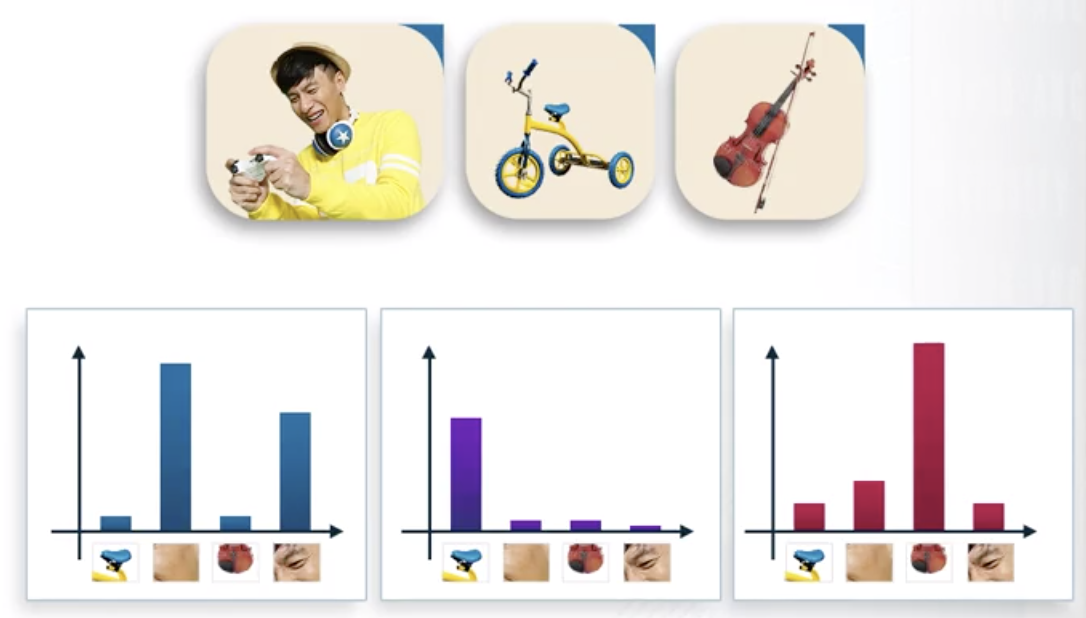
image-20210127121545310

  • 사람 얼굴
    • 사람의 눈 > 가중치 높음 (실제로 존재)
    • 자전거 안장, 바이올린 밑동 > 가중치 낮음 (없음)
    • 반응성의 측면에서 안장, 바이올린 밑동은 사람 이미지에서 “잘 보이지 않는 부분적인 이미지”가 됨

각각의 워드들에 대해서:

  • 반응성(가중치)을 모두 계산
  • 히스토그램 형식으로 시각화
  • 각 이미지의 특징에 해당하는 word에 대해서는 높은 가중치, 특징에 해당하지 않는다면 낮은 가중치

이렇게 얻어진 히스토그램 = “Bag of words”

  • 이미지에 포함된 모든 픽셀을 활용하는 것보다, 단순한 피쳐로 이미지를 분류할 수 있음
    • 샘플 3개
      • 사람, 자전거, 바이올린 이미지
    • 피쳐 4개
      • 자전거 안장, 사람 피부, 바이올린 밑동, 사람 눈
    • 주어진 데이터가 비선형 특성을 갖고 있음에도 잘 분류할 수 있는 방법

Feature Engineering의 Convolution

  • 특정 이미지가 주어졌을 때, 개별 픽셀 값이 물체를 분류하는 데 큰 의미가 있는 것은 아님
  • 색상값을 제외하고 강아지와 고양이를 구분하는 방법?

image-20210127122307577

강아지 vs. 고양이

  • 눈의 형태가 특징적으로 다르다
  • 귀의 형태가 특징적으로 다르다
    • 픽셀 밸류를 활용하기보다, 상관관계를 주로 탐색함

image-20210127122509714

위와 같은 특징적인 픽셀 영역 = 복셀

  • 복셀 정보를 활용하여, 클래시피케이션 문제나 리그레션 문제 등을 해결함
  • 복셀을 고려하기 위하여 주로 사용되는 방법론 = convolution

Convolution

  • 특정 필터가 제공되면, 필터를 이미지에 그대로 적용하여 필터 반응성을 확인
  • “필터”는 무엇이고, “필터 반응성” 이란 무엇일까?

1-D Convolution Example

\[[0 \ 1 \ 1 \ 2 \ 3 \ 5 \ 8 \ 13]\]

필터에 컨볼루션을 적용한다는 것의 의미

  • 각각의 픽셀값을 filter에 곱하고, 그 결과값들을 모두 더하는 것

필터의 종류

  • Identity Filter $[0 \ 1 \ 0]$
    • 양쪽의 엘러멘트가 0, 가운데만 1인 기본 필터
    • 이미지나 데이터에 적용하면 입력된 데이터 혹은 그림을 그대로 출력
    • 모든 엘러멘트들에 대응되는 픽셀값들을 곱하고 거기에 대응되는 곱해진 결과값들을 모두 더한 값을 바로 가운데 픽셀에 입력
    • 양쪽 엘러멘트가 모두 0이므로 양쪽 픽셀을 고려하지 않고, 가운데 픽셀이 그대로 유지되는 결과를 출력
    • 컨볼루션을 적용할 필요가 없음
  • Translation Filter $[0 \ 0 \ 1]$
    • 왼쪽, 가운데가 0, 오른쪽 1개만 1인 필터
    • 오른쪽에 있는 픽셀값이 가운데로 배정된다는 의미
    • 컨볼루션 적용 시, 이미지 혹은 데이터가 왼쪽으로 한 칸씩 당겨짐
  • Local Average $[\frac{1}{3} \ \frac{1}{3} \ \frac{1}{3}]$
    • 모든 엘러멘트 값이 1/3로 동일하게 설정
    • 자기 자신의 위치와 양쪽 위치에 있는 값들을 모두 더해서 평균을 내는 것
    • 노이즈 줄어드는 효과를 볼 수 있어 머신러닝 기법에서 항상 활용
  • First Derivative $[-1 \ 0 \ 1]$
    • 미분하는 형태를 갖추고 있고, 모든 엘러멘트들의 총합은 0
    • 현재 최종적인 결과값이 왼쪽 픽셀과 오른쪽 픽셀의 차이가 됨
    • 영상이나 이미지 데이터의 왼쪽, 오른쪽의 차이를 계산할 때 first derivative filter 사용함
  • Gaussian $exp(\frac{-i^2}{2\sigma^2})$
    • 기존 애버리지 필터의 경우 가중치가 모두 동일하게 계산
    • 가우시안 필터는 자신에 대해 가중치가 더 크고 멀리 떨어져 있으면 가중치가 점점 작아짐
    • 대표적인 blurring 필터
  • Sharpen convolution $[-1 \ 3 \ -1]$
    • 가운데 엘러먼트는 3이고, 그 근처에 배치된 엘러먼트가 모두 -1로 그 차이를 최대한으로 하는 방식으로 구성
    • 서로 붙어 있는 픽셀들 간의 차이값이 더욱 강조됨
    • 애버리지 필터나 가우시안 필터의 정반대 효과 > 경계선 강조
  • Laplacian $[-1 \ 2 \ -1]$
    • first derivative 필터와 상당히 유사한 결과를 보여주는 필터
    • Sharpen convolution과 형태 비슷하지만, 모든 엘러먼트들을 합했을 때 0이라는 결과값을 보여줌
    • 어떤 경계선에 해당되는 픽셀이 좀 더 강조되고, 그렇지 못한 영역들은 0에 가까운 값을 가지도록 결과값(이미지) 출력

Boundary Issue

어떤 필터를 적용할 때, 가운데 픽셀에 weighted sum이 배정된다. 왼쪽 혹은 오른쪽 픽셀이 없다면 어떻게 계산해야 할까?

기본적으로 계산 불가능

  • 필터를 적용할 때마다 이미지가 점점 작아짐
  • 예) 3X1 컨볼루션 필터를 적용할 때 마다 2픽셀씩 사라짐
    • 필터가 적용될 때마다, 어떤 가상의 값을 배정하는 식으로 문제를 해결함

가장자리에 배정할 수 있는 값?

Zero Padding Replicate Mirror
없는 픽셀값을 0으로 배정 현재 왼쪽 끝에 있는 픽셀값을 그대로 복사 현재 새로 생긴 픽셀 값의 정반대에 있는 값을 배정
  • 위 방법을 적용하면 필터를 적용해도 이미지 크기가 줄어들지 않음

이미지 데이터의 Feature 추출 과정

2D Convolution

\[z[i_1, i_2]=\sum_{j_1=-m}^m\sum_{j_2=-m}^mw[j_1, j_2]x[i_1+j_1,i_2+j_2]\]
  • 필터 각각의 픽셀에 대응되는 필터값과 이미지값들을 모두 곱한 다음, 그 결과값들을 더한 값을 바로 그 가운데에 위치한 최종적인 필터 결과값에 배정
  • 2D 이므로 2개의 좌표값을 고려하여 최종적인 값을 도출함

3D Convolution

\[z[i_1, i_2, i_3]=\sum_{j_1=-m}^m\sum_{j_2=-m}^m\sum_{j_3=-m}^mw[j_1, j_2, j_3]x[i_1+j_1, \ i_2+j_2, \ i_3+j_3]\]
  • 일반적으로 이미지는 빨간색, 초록색, 파란색 (RGB) 총 세 가지 컬러를 가지고 있으므로 3D 이미지
  • 각각에 대응되는 filter 값과, 거기에 대응되는 이미지값들을 모두 곱한 다음 더하고, 그 가운데에다 결과값을 배정하면 우리가 원하는 filter 결과값을 얻을 수 있다
  • 여기서도 마찬가지로 패딩 적용해 이미지 크기 감소 방지

가장 대표적인 이미지 컨볼루션 필터

Gaussian Filter

  • 어떤 이미지의 자잘한 노이즈나 경계선을 최대한 누름으로써, 좀 더 전체적인 이미지의 형태를 파악함
  • blurring / Averaging

image-20210127130430258

Laplacian of Gaussian (LoG)

  • 이미지 경계선 위주로 탐색할 수 있는 알고리즘
  • 경계선의 형태를 비교하기 위해 경계선을 추출

image-20210127130615388

Gabor Filters

  • 경계선을 알아내는 것과 더불어, 그 경계선의 방향까지 파악
  • 여러 가지 미분되는 형태의 컨볼루션 필터를 이미지에 적용
    • 반응성이 가장 큰 것을 선택하여 활용

image-20210127130646571

Weighted Histogram

  1. 위에서 소개한 필터를 적용, 필터 반응성 기반으로 얻은 이미지를 그대로 feature로 사용
  2. 필터 적용하여 이미지를 얻은 뒤, Bag-of-word 방식으로 한번 더 정리

Weighted Histogram

Bag-of-word 방식으로 더 정리해 본다면?

  • 히스토그램을 그려서 필터 반응성을 살필 수 있도록 여러 개의 필터를 둠
  • 각각의 필터에 대한 서로 다른 히스토그램을 그릴 수 있음
  • 전체 이미지에 대해 반응성의 히스토그램을 그리는 방식

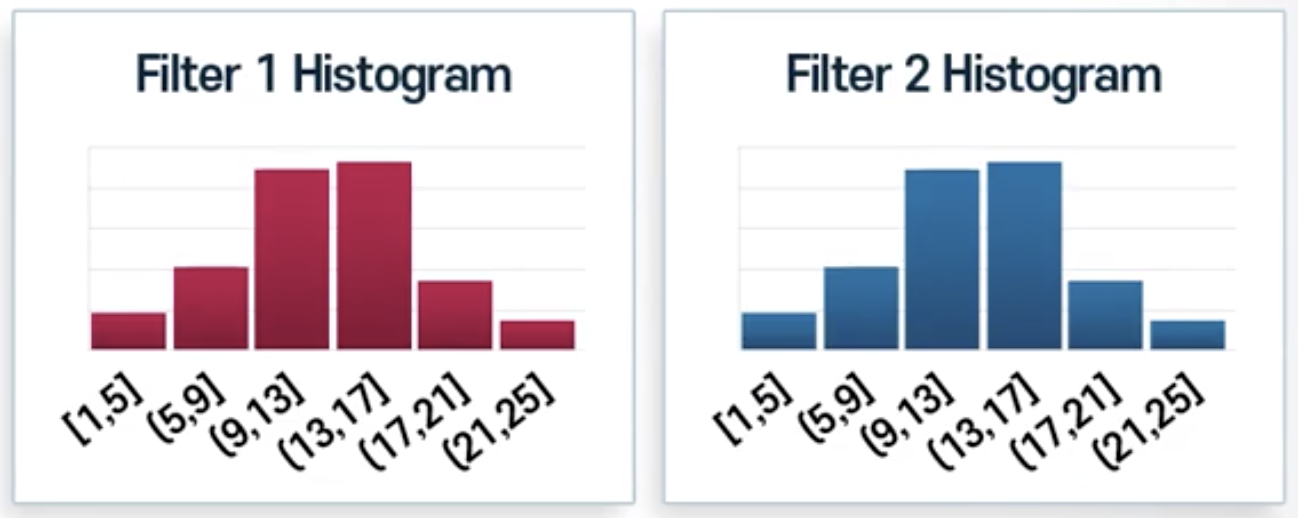
image-20210127131101210

특징을 기반으로 이미지나 카테고리 등을 분류하는 bag-of-word 방식

이미지의 pixel values는 비선형 특성이더라도, 히스토그램화 함으로써 선형 모델로도 학습 가능하도록 변형

K-mooc, 딥러닝의 깊이 있는 이해를 위한 머신러닝, 중앙대학교 첨단영상대학원 영상학과 최종원 교수님

*그래프 이미지 출처: 강의자료