이번 글에서는 머신러닝 프로세스에서 큰 비중을 차지하는 데이터 전처리의 개념을 소개하고자 합니다. 데이터 전처리를 정의하는 것부터 시작해봅시다.
차원의 저주에서 벗어나자,,!!
What is Data Preprocessing?
데이터라는 말을 들으면, 우리는 대개 수많은 행과 열로 이루어진 거대한 데이터셋을 떠올립니다. 그럴 법도 하지만, 항상 그렇지만도 않습니다. 데이터는 매우 다양한 형태로 나타날 수 있습니다: 구조화된 표, 이미지, 오디오 파일, 비디오, 기타 등등.
기계는 자유롭게 작성된 글이나 이미지, 비디오를 있는 그대로 이해하지 못합니다. 기계가 이해하는 것은 0과 1 뿐이다. 따라서 이미지를 슬라이드쇼에 올려놓고 기계가 학습하길 바라긴 힘들 겁니다.
어떠한 머신러닝 프로세스에서도, 데이터 전처리는 기계가 잘 알아들을 수 있는 방식으로 데이터를 형성하거나 해석하는 단계에 해당한다. 데이터 전처리를 거친 데이터의 피쳐 값들은 알고리즘이 쉽게 해석할 수 있다.
Features in Machine Learning
데이터셋은 기록, 점, 벡터, 패턴, 사건, 샘플, 관측 등으로도 불리는 데이터 객체의 집합으로 볼 수 있습니다. 데이터 객체란 객체의 기본 특성들을 묘사하는 수많은 피쳐들에 의하여 설명됩니다. 물체의 질량, 사건이 발생한 시간 등이 피쳐가 될 수 있습니다. 피쳐는 변수(variable), 특징(characteristics), 필드(field), 특성(attribute) 또는 차원(dimension)이라고 부르기도 합니다.
As per Wikipedia.
피쳐 = 독립된 측정가능한 속성 또는 관측된 특징적인 현상
예를 들어, 색상, 주행거리 그리고 엔진 마력은 자동차의 피쳐로 고려해볼 수 있겠습니다. 그 외에도 데이터를 다루다 보면 마주칠 수 있는 매우 다양한 종류의 피쳐들이 존재합니다.
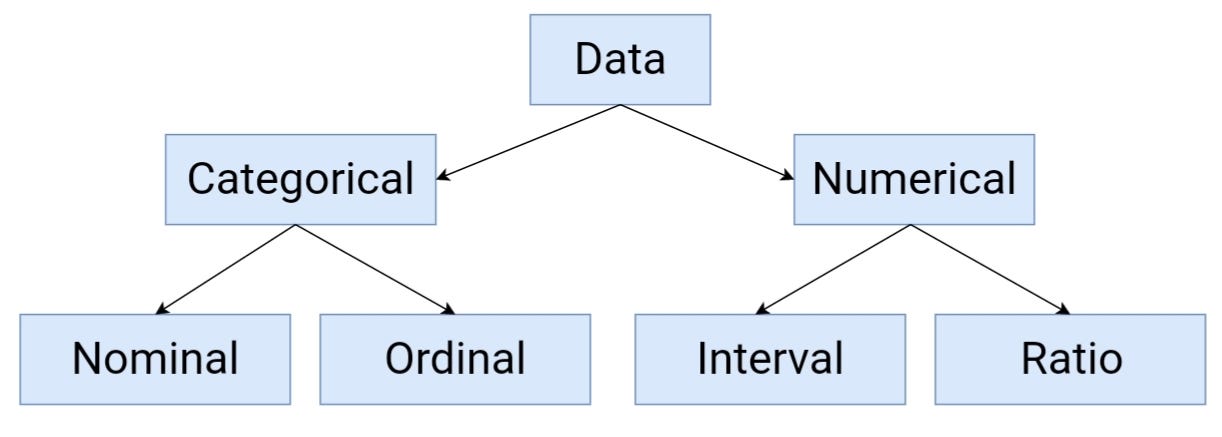Statistical Data Types
피쳐를 크게 두 가지로 구분해 보면:
- Categorical : 정의된 집합으로부터 가져온 값들. 예를 들어 한 주의 요일들 {월요일, 화요일, 수요일, 목요일, 금요일, 토요일, 일요일}은 카테고리 피쳐가 됩니다. 왜냐하면 이러한 값들은 언제나 요일이라고 정의된 집합에서 가져오기 때문이죠. 다른 예로는 Boolean 셋을 들 수 있습니다: {True, False}
- Numerical : 실수 또는 정수값. 숫자로 표현되며 숫자의 거의 모든 특성들을 지니고 있습니다. 하루에 걷는 걸음 수 또는 자동차를 주행할 때의 속도 등이 이에 해당합니다.
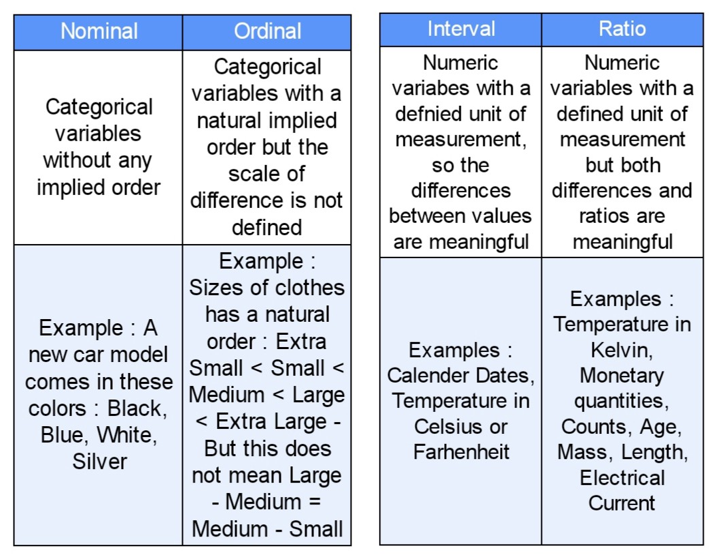Feature Types
이제 기초적인 내용을 알았으니 데이터 전처리에 대해 본격적으로 알아봅시다. 그러나 소개할 방법 모두가 모든 문제에 동일하게 적용되는 것은 아님을 기억해 주세요. 우리가 다루고 있는 데이터의 종류에 크게 의존하는 만큼, 각각의 데이터셋은 몇 개의 방법만 필요로 할 수 있습니다.
일반적인 데이터 전처리의 방법들은 다음과 같습니다:
- Data Quality Assessment
- Feature Aggregation
- Feature Samping
- Dimensionality Reduction
- Feature Encoding
Data Quality Assessment
데이터는 때로 여러 출처에서 가져오게 됩니다. 그다지 좋은 품질이 아닐 수도 있고, 저장 형식이 너무 다를 수도 있겠죠. 업무시간의 절반 이상을 데이터 품질 문제에 붙잡힐 수도 있습니다. 모든 데이터가 완벽하길 기대하는 것은 단순하게 불가능합니다. 휴먼 에러, 측정 기기의 한계, 데이터 수집 프로세스 결함 등등. 이러한 문제를 해결하는 몇 가지 방법들을 살펴보겠습니다.
Missing Values
데이터셋에서 미싱 밸류는 흔하게 찾아볼 수 있습니다. 데이터 수집 과정에서 누락되거나, 어쩌면 데이터 검증 규칙 때문일 수도 있지만, 그것과 상관없이 미싱 밸류는 어떻게든 손을 써줘야 하겠죠.
-
미싱 밸류가 존재하는 행 삭제하기
단순하고 때때로 효과적인 전략. 그러나 너무 많은 행을 삭제해야만 한다면 조심하세요. 하나의 피쳐를 구성하는 대부분의 값들이 미싱 밸류라면, 피쳐를 통째로 삭제할 수도 있을 겁니다.
-
미싱 밸류 평가하기
전체 데이터에서 미싱 밸류가 차지하는 비율이 납득할 만 하다면, 미싱 밸류를 채워넣기 위해 단순한 보간법(interpolation methods)을 실시할 수 있습니다. 그렇지만 속한 피쳐의 평균값, 중간값 또는 최빈값이 가장 흔하게 사용되는 방법입니다.
Inconsistent values
적절하지 않은 데이터가 입력된 상황도 흔하게 일어납니다. 예를 들면, ‘주소’ 필드에 ‘전화번호’ 값이 저장된 경우. 휴먼 에러 때문일 수도 있고, 수기 형태의 자료를 스캔하는 과정에서 잘못 읽혔을 수도 있습니다.
- 각 피쳐에 어떠한 자료형이 들어가야 하는지, 그 규칙은 모든 데이터 객체에 일괄적으로 적용되는지 등을 파악하는 data assessment를 본격적인 작업 전 반드시 수행할 것을 추천합니다.
Duplicate Values
데이터셋은 중복된 값들이 있을 수 있습니다. 같은 사람이 1회 이상 서류를 중복 제출한다거나 할 때 발생할 수 있습니다. deduplication이라는 용어는 중복값을 처리하는 과정이라는 의미로 사용되기도 합니다.
- 대부분의 경우, 중복값은 머신러닝 알고리즘이 동작할 때 특정 데이터 객체에 추가적인 가중치 또는 편향을 부여하지 않도록 삭제 처리합니다.
Feature Aggregation
Feature Aggregation은 데이터를 보는 더 좋은 관점을 얻기 위하여 정보값들을 취합하는 작업을 말합니다. 예를 들어, 수년 동안 다양한 상점에서 발생하는 상품 판매를 매일 기록하고 있다고 해 봅시다. 이러한 데이터들을 모든 상점들의 월별 또는 연도별 거래라는 단일한 데이터로 취합하는 것은 어떤 도움이 될까요? 이는 특정 상점에서 매일 발생하는 수백 수천 건의 거래들을 감소시키는 효과를 가지며, 따라서 데이터 객체의 숫자를 줄이게 됩니다.
- Feature aggregation은 메모리 소비량 및 처리시간을 줄여 줍니다.
- Feature aggregation으로 얻어진 그룹 또는 취합된 데이터의 행동이 개별 데이터 객체보다 더 안정적이며, 이는 데이터에 대한 고수준의 관점을 제공합니다.
Aggregation from Monthly to Yearly
Feature Sampling
샘플링은 분석하고자 하는 데이터셋의 일부를 선택할 때 흔하게 사용되는 기법입니다. 대부분의 경우, “완벽한” 데이터셋을 가지고 작업하려 하는 것은 메모리 리소스 및 시간비용 관점에서 가성비가 최악입니다. 샘플링 알고리즘을 사용함으로써, 우리는 더 좋지만 비싼 머신러닝 알고리즘을 사용할 만 한 크기까지 데이터셋의 몸집을 줄일 수 있게 됩니다.
여기서 핵심 원칙은 샘플링의 결과물이 데이터셋 원본의 속성들에 근사하는 속성들을 갖도록 수행되어야 한다는 것, 즉 대표성을 갖고 있어야 한다는 겁니다. 이를 위해 올바른 샘플 사이즈와 샘플링 전략을 선택해야 하겠죠. Simple Random Sampling은 임의의 특정 데이터셋을 선택할 확률은 모두 같다고 가정합니다. 이 샘플링 방법을 두 가지로 구분해 보면:
- Sampling without Replacement : 각각의 선택된 아이템은 전체 데이터셋을 이루는 객체집합으로부터 제거됩니다.
- Sampling with Replacement : 각각의 선택된 아이템은, 선택된 이후에도 전체 데이터셋으로부터 제거되지 않는다. 이는 1회 이상 샘플링될 수 있음을 의미합니다.
Simple Random Sampling이 멋진 2가지 테크닉을 제공하고 있지만, 데이터셋이 심하게 들쑥날쑥한 객체 타입을 포함하고 있을 때엔 대표성이 없는 샘플을 내놓게 되고 맙니다. 샘플이 모든 객체 타입에 대하여 적절한 대표성을 갖지 못한다면 문제가 되겠죠. 우리가 가진 데이터셋이 불균형적인 데이터셋이라면 분명 대표성을 가진 샘플이 필요할 겁니다.
불균형적인 데이터셋은 특정 클래스 인스턴스의 갯수가 다른 클래스들보다 눈에 띄게 큰 탓에, 전체 데이터셋의 균형을 무너뜨리며 ‘더 희소한’ 클래스들을 만들어내는 데이터셋을 말한다.
‘더 희소한’ 클래스들은 샘플 내에서 적절하게 대표되어야 하며, 이는 매우 중요한 문제입니다. 희소 클래스들이 존재할 경우 우리는 Stratified Sampling을 사용할 수 있는데, 이 방법은 미리 지정한 오브젝트 그룹들을 갖고 시작합니다. Stratified Sampling도 2가지 버전이 존재하는데요. 첫번째는 단순한 버전으로, 클래스의 크기와 상관없이 모든 클래스들로부터 같은 숫자의 오브젝트를 뽑는 겁니다. 샘플링에 관해 더 알아보고 싶으면 아래 글을 참고해 주세요.
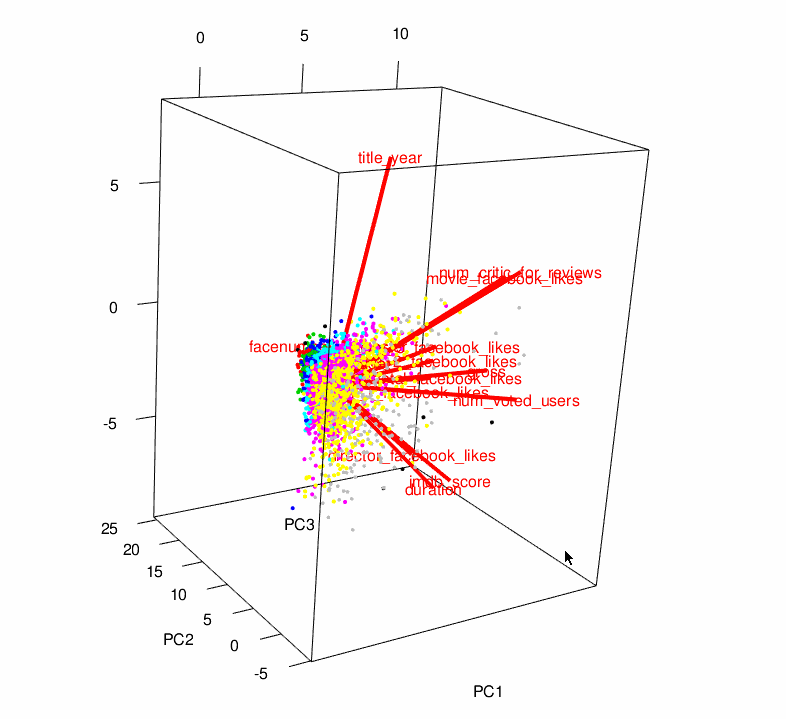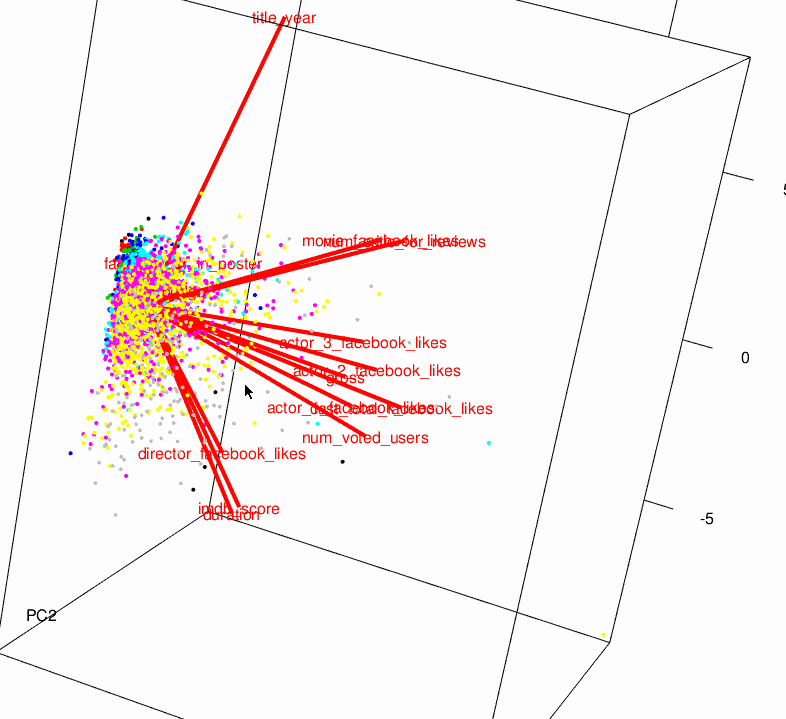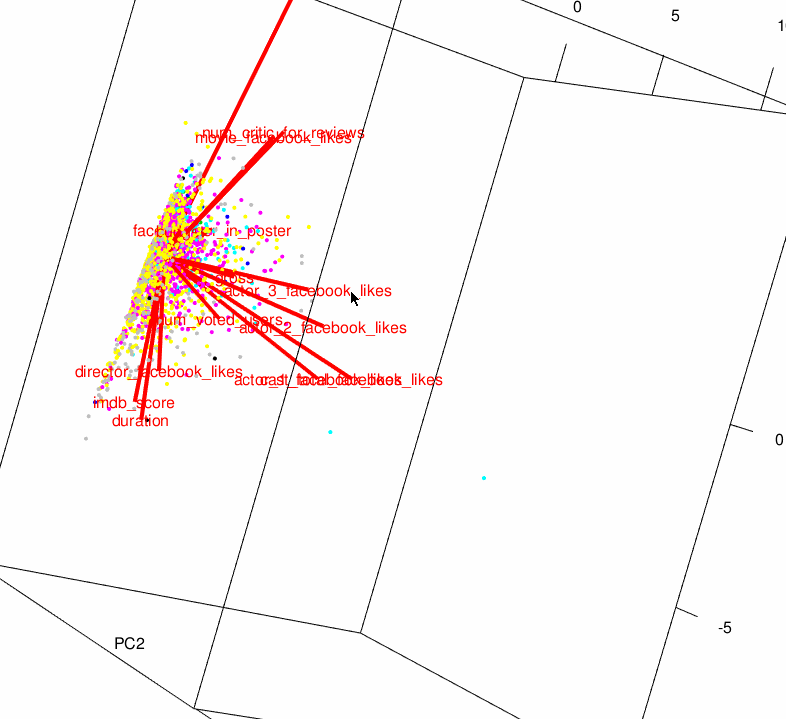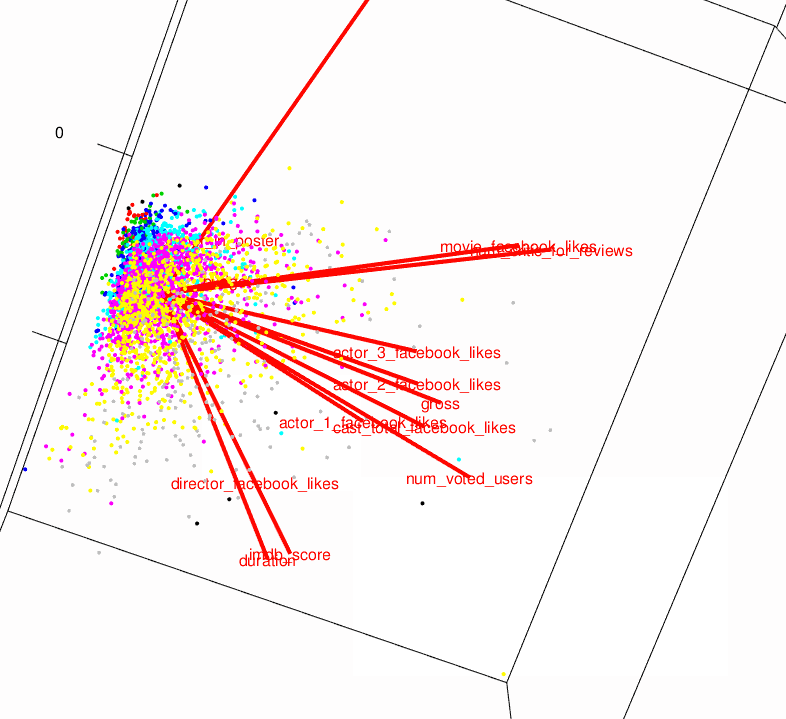
Dimensionality Reduction
현실세계의 데이터셋 대부분은 피쳐 숫자가 많습니다. 이미지 전처리 문제를 예로 들어보자면, 우리는 차원 이라고도 불리는 수천개의 피쳐들을 다뤄야 할 겁니다. 차원 축소라는 말 그대로, 차원 축소는 피쳐 갯수를 줄이는 것을 목적으로 합니다. 그러나 단순히 피쳐셋에서 피쳐 샘플을 아무거나 뽑는 것은 아닙니다. 우리가 쓸 방법은 Feature Subset Selection 또는 단순하게 Feature Selection이라 불리는 방법입니다.
개념적으로, 차원 이란 데이터셋이 위치하고 있는 기하학적 평면의 숫자를 의미하며, 종이 위에 그릴 수 없을만큼 차원이 높을 수도 있습니다. 차원 갯수가 많을수록, 데이터셋도 복잡해집니다.
The Curse of Dimensionality
차원의 저주란, 데이터의 차원이 높아짐에 따라 데이터 분석이 매우 매우 어려워지는 현상을 말합니다. 차원의 갯수가 증가하면서 각각의 데이터가 점유하는 평면의 갯수가 증가하며, 따라서 데이터 간의 거리가 점점 더 멀어지게(sparse) 됩니다. 이는 곧 모델링 및 시각화하기 어렵게 됨을 의미합니다.
Representation of components in different spaces
차원 축소가 본질적으로 수행하는 일은 데이터셋을 저차원 공간으로 매핑(mapping)하는 것이며, 시각화가 간편한 2차원이라면 더할 나위 없을 겁니다. 차원 축소 기법의 기본 목적은 기존 피쳐들을 조합하여 새로운 피쳐들을 만들어냄으로써, 데이터셋의 차원을 줄이는 것입니다. 말하자면 고차원 피쳐 공간이 저차원 피쳐 공간으로 매핑(mapping)되는 것이죠. Principal Component Analysis (주성분분석) 그리고 Singluar Value Decomposition(고윳값분해)은 널리 사용되는 차원 축소 기법입니다.
차원 축소의 주요 장점은 다음과 같습니다:
- 데이터 분석 알고리즘은 데이터 차원이 낮을 때에 더 잘 동작한다. 대체로 중요하지 않은 피쳐와 소음(아웃라이어)들이 사라졌기 때문입니다.
- 저차원 데이터 위에서 구축된 머신러닝 모델은 이해하기 쉽고 설명하기 쉽습니다.
- 게다가 데이터 시각화가 한결 쉬워지기도 합니다. 피쳐는 언제나 시각화 목적을 위해 2개(2차원), 3개씩(3차원) 묶일 수 있는데요. 피쳐셋이 그다지 크지 않을수록 이러한 시각화의 설명력도 높아집니다.
Feature Encoding
Feature Encoding
앞서 언급했듯 데이터 전처리의 목적은 기계가 이해하기 좋은 상태로 데이터를 인코딩(변환)하기 위해서입니다.
Feature encoding은 본래의 의미를 유지하면서도 머신러닝 알고리즘 친화적으로 데이터를 변환하는 작업을 의미한다.
Feature encoding을 수행할 때 기본적으로 따라오는 규칙이 있습니다. 불연속적인 변수에 대해서는:
- Nominal : 의미가 보존된다면 어떠한 one-to-one 매핑도 가능합니다. 예를 들면, One-Hot Encoding과 같은 값들의 순열 형태가 있습니다.
- Ordinal : 값들의 순서가 보존되는 변환. ‘대-중-소’라는 구분은 $<\text{new value} = f(\text{old_value})>$ 등과 같이 새로운 함수의 도움으로 동등한 크기의 차이로서 표현될 수 있습니다. 예를 들면, {2, 1, 0} 또는 {3, 2, 1}.
One-hot encoding of the data
연속적인 변수(실수)에 대해서는:
- Interval : $<\text{new_value}=(a*\text{old_value}+b) \ for \ a, \ b \ being \ constants>$ 와 같은 단순한 수학적 변환. 예를 들어, Fahrenheit 온도와 Celsius 온도는 이러한 방식으로 인코딩 될 수 있습니다.
- Ratio : 특정한 기준, 척도에 따라 커졌다 작아지는 실수 변수. $<\text{new_value}=a*\text{old_value}>$ 같은, 마찬가지로 단순한 수학적 변환법을 적용합니다. 예를 들어 길이는 미터나 피트로 측정될 수 있으며, 돈은 다른 통화로 측정될 수 있습니다.
Train / Validation / Test Split
Feature encoding까지 완료되었다면, 우리의 데이터셋은 이제 신나는 머신러닝 알고리즘에 넣을 준비를 거의 마쳤습니다. 그러나 어떤 알고리즘을 사용해야 할 지 결정하기 전에, 데이터셋을 2개나 3개의 작은 데이터셋으로 쪼갤 것을 권장합니다. 머신러닝 알고리즘, 또는 그에 준하는 어떤 알고리즘은 우선적으로 가용한 수준에서 학습되어야 하고, 이후 검증과 시험을 통과해야만 합니다. 실제 세상의 데이터와 맞서 싸우러 나가기 전에 말이죠.
Training Data
학습 데이터는 머신러닝 알고리즘이 실제로 모델을 구축하기 위해 학습하는 데 사용하는 데이터입니다. 모델은 데이터셋과 함께 데이터셋의 다양한 특성들과 데이터 내부의 상호관계를 학습 하게 되는데요. 특히, 데이터 내부에 존재하는 복잡한 상호관계/상호의존성(intricacies)은 오버피팅 또는 언더피팅 이라는 문제를 발생시키는 원인이 되기도 합니다.
Validation Data
검증 데이터는 우리가 학습시킨 다양한 모델들을 검증하는 데 사용하는 데이터입니다. 쉽게 말해, 우리는 모델 하이퍼파라미터를 선택하고 개선하기 위하여 검증 데이터를 사용합니다. 머신러닝 모델은 검증 데이터를 학습 하는 것이 아니라, 더 나은 하이퍼파라미터 상태에 도달하기 위해 사용 한다는 점을 기억하세요.
Test Data
테스트 데이터는 우리의 모델 가설을 마지막으로 테스트할 때 쓰는 데이터입니다. 모델이 만들어지고 하이퍼파라미터 최적화가 완료될 때까지, 테스트 데이터는 완전히 숨겨진 상태로 사용되어선 안 됩니다. 그렇게 해야만, 모델이 현실 세계의 데이터에 대하여 어떤 성능을 내는지 정확하게 측정할 수 있으니까요.
Data Split into parts
Split Ratio
데이터는 구축하고자 하는 모델과 데이터셋에 따라 크게 달라지는 split ratio 에 따라서 나누어지게 됩니다. 만약 우리가 가진 데이터셋과 모델이 매우 많은 학습을 필요로 한다면, 대개 학습 데이터 비중을 더 많이 할당해야 합니다. 일반적으로 수천 개의 피쳐를 학습해야만 하는 문자열, 이미지 또는 비디오 데이터가 이러한 예에 해당할 겁니다.
만약 모델이 최적화될 수 있는 수많은 하이퍼파라미터를 갖고 있다면, 검증 데이터 할당량을 늘리는 것을 권장합니다. 하이퍼파라미터 숫자가 적은 모델은 상대적으로 조정과 변경이 쉬우므로 검증 셋은 적어도 충분합니다.
머신러닝의 다른 것과 마찬가지로, split ratio는 우리가 해결하려고 하는 문제에 따라 크게 달라질 수 있습니다. 모델과 데이터셋에 대하여 가능한 모든 검토를 마친 뒤에 결정할 것을 권합니다.
This is it!
이번 글을 통해, 머신러닝 프로세스에서 매우 중요한 절차인 데이터 전처리의 개념을 소개해 드렸습니다. 도움이 되었기를 바랍니다.
source : Data Preprocessing:Concepts by Pranjal Pandey