선형 모델은 데이터 노이즈 취약성 외에도 다른 한계점을 가지고 있습니다. 이번 포스트에서는 선형 모델의 멀티 클래스 문제와 오버피팅 문제를 살펴보고, 개선 방법은 무엇인지 알아봅니다.
앞서 작성된 글:
선형 모델의 한계점
- 클래스가 많을 때 Classification Model 활용 어려움
- 오버피팅
살펴볼 내용들
- Multi-class 문제는 어떻게 해결할까
- p-norm이란 무엇일까
- Regularization이란 무엇이고 어떤 것들을 써야 할까
Multi-class 문제는 어떻게 해결할까
Multi-class Classification: one-vs-all
one vs. all
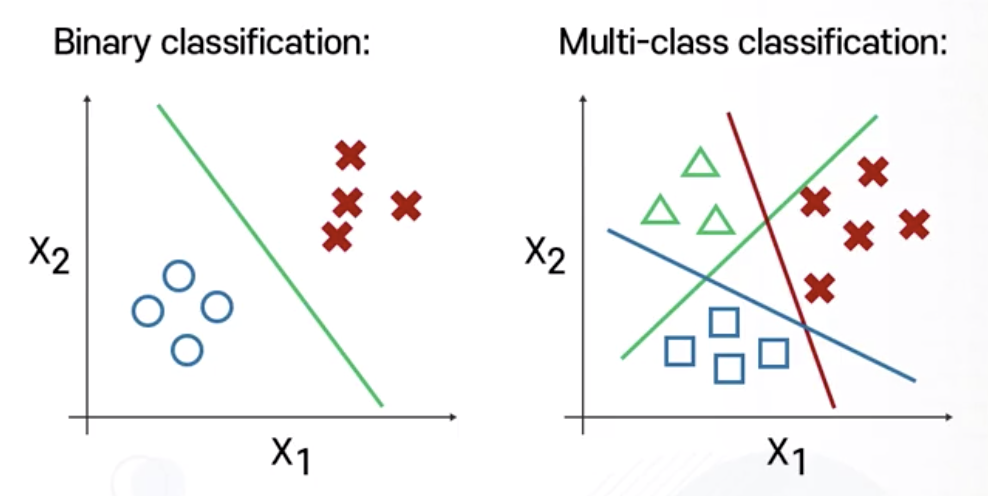
- 한 개 클래스와 나머지 모든 클래스를 구분하는 Linear Classification Model 탐색
- 클래스 갯수가 3개면 Linear Classification Model 3개
- class 1 vs. class 2, 3
- class 2 vs. class 1, 3
- class 3 vs. class 1, 2
- 총 k개의 클래스가 있다면 k개의 Linear Classification Model 필요
- 총 k개의 Classifier가 확보된다면 새로운 샘플의 추정 라벨은?
- 주어진 k개의 Classifier를 모두 적용한 후, 가장 높은 점수를 갖는 클래스 C를 배정
p-norm이란 무엇일까
Distances > p-norms
- 벡터 간의 거리를 계산하는 norm을 p-norm으로 통칭함
L2-norm
- Euclidean distance
- 어떤 두 개의 feature가 존재할 때 두 개의 feature 사이의 기하학상 거리
- Euclidean distance 외에도 다양한 distance 계산 방법 존재
- L2-norm
- L1-norm
- 0-norm
- $\infty$ norm
- cosine distance
- …
- 주어진 데이터 또는 머신러닝 기법에 따라서 적합한 계산법을 선택해야 함
L1-norm
각각의 에러값에 절대값을 취한 후 합산
- robust regression에서 활용
- 아웃라이어가 존재하더라도 강인하게 작동
특정 feature가 전반적으로 너무 퍼져 있는(sparse) 상황
- 해당 feature에 대한 신뢰도가 매우 낮을 가능성 큼
- 위 상황에서 L2-norm 적용
- 다른 inlier feature들의 값이 제곱에 의해서 상대적으로 무시당하는 경향 발생
- L1-norm 적용
- outlier feature dimension을 일정 부분 무시할 수 있음
L0-norm
입력된 에러값이 0이면 유지, 0이 아니면 1이 더해지는 형태
- 0-1 loss와 관련됨
- $\boldsymbol{\delta}(\cdot)$
- 입력된 조건문이 성립하면 1 출력
- 입력된 조건문이 성립하지 않을 경우 0 출력
$\boldsymbol{\infty}$ norm
노이즈에 오히려 관심을 갖도록 만드는 방식
\[||r||_0=\underset{j}\max|r_j|\]- 여러 개의 에러 중 최댓값을 출력
- 최대 에러값 = 아웃라이어
- 아웃라이어에 좀 더 집중하는 objective function
- 아웃라이어가 거의 배제되어 있는 상황에서 최대한 발생할 수 있는 에러를 최소화하고 싶을 때
- $\boldsymbol{\infty}$ norm을 적용하여 최대한의 에러가 발생하는 것을 줄이는 방향으로 학습할 수 있음
Frobenius norm
현재까지 다룬 p-norm은 벡터에 대해서만 계산 가능한 개념
- Frobenius norm = 매트릭스에 대한 한 개의 norm 계산
L2-norm과 형태 매우 유사하여 L2-norm 형태로도 표현 가능
- 입력된 매트릭스의 각각의 컬럼에 대해 L2-norm의 제곱 계산
- 각 컬럼의 L2-norm 제곱값을 합한 뒤 square root
Encouraging invariance
샘플 간 상관관계를 distance로 생각해 보기
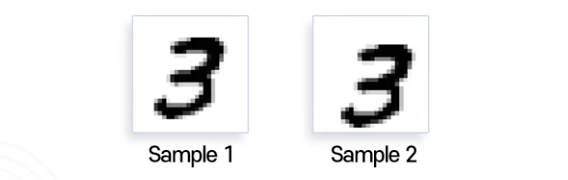
- 사람 입장에서 sample 1과 sample 2는 매우 비슷하다고 인식
- 컴퓨터 입장에서 ‘비슷하다’ = ‘거리가 가깝다’
- L1-norm 또는 L2-norm으로 거리를 계산한다면?
- 동일한 픽셀 위치에 서로 비슷한 값을 갖고 있으므로
- distance가 상대적으로 굉장히 크게 계산된다
극단적인 예시를 들자면,

- 사람 입장에서 여전히 세 개의 sample이 비슷하게 인식
- 비슷한 정보를 가지고 있다
- 정보로서의 distance 거리가 가깝다
- 컴퓨터 입장에서
- 흰색 > 1에 가까운 값
- 검은색 > 0에 가까운 값
- $\text{distance(sample3 - sample1)}$ 엄청나게 커짐
- 비슷하지 않은 정보로 인식
- distance가 멀다고 인식
- 사람은 비슷하다 인식해도 컴퓨터는 작은 변화에 민감하게 반응
- sample 1 vs. sample 2 이미지 좌우 반전 상태
- sample 3이 15도 가량 회전 > 컴퓨터 입장에서 distance 증가
- scale change가 발생하여도 distance 증가
- 어떻게 하면 사람의 관점을 컴퓨터에게 학습시킬 수 있을까?
- 여러 가지 feature들이 변형되는 상황에 강인한 distance를 선택하여 적용
- 상당히 어려운 문제
- 어떤 distance를 사용해도 거리 좁히기 쉽지 않음
- Data Augmentation
- 기존의 데이터를 랜덤하게 좌우 반전, 회전시키거나 색깔을 뒤집는 등 가공하여 학습 데이터에 추가
- 여러 가지 feature들이 변형되는 상황에 강인한 distance를 선택하여 적용
Data Augmentation
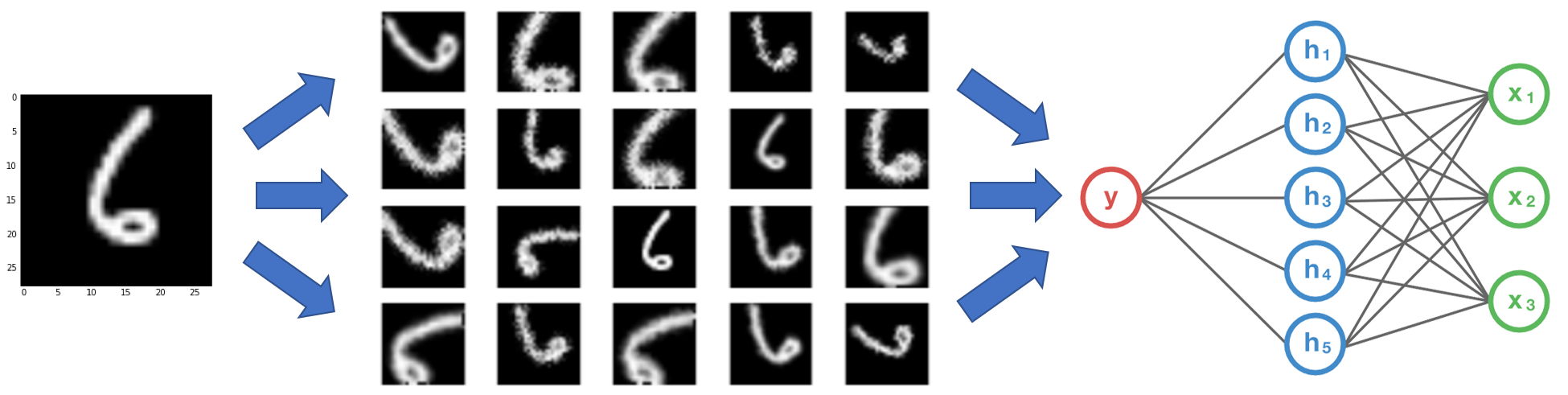
- 1개의 데이터로부터 많은 가공 데이터를 생성
- 이러한 가공된 데이터를 학습 데이터의 일부로 활용
- 더 다양한 상황의 데이터를 확보하는 효과
이미지 샘플이 좌우 이동 또는 회전되어 있는 형태이더라도 좋은 성능의 머신러닝 결과를 얻을 수 있음
Regularization이 무엇이고 어떤 것을 써야할까?
L2-Regularization
오버피팅
- 학습 데이터에 대해서만 모델 성능이 좋음
- 중요한 테스트 데이터에 대해서는 성능이 떨어짐
- w값 중에 하나가 매우 커지는 상황
- 특정 w가 커진다는 의미?
- 모델이 w에 해당되는 feature를 중점적으로 보고 있다
- 그 외의 feature들이 상대적으로 무시되고 있다
중점적으로 보는 feature의 중요성이 낮은 새로운 sample이 들어온다면?
- 중점 feature 외에 다른 정보들을 이용해 sample 분류해야 함
- 이미 학습 데이터에서 중점 feature의 w값이 커져 있으므로 다른 정보들을 판단하는 능력이 매우 떨어진 상태
- 이러한 상황이 Linear Model에서 발생하는 대표적인 오버피팅 문제
L2-Regularization
오버피팅을 해결하는 가장 손쉬운 방법 중 하나
\[f(\mathbf{w})=\frac{1}{2}\scriptstyle{\sum_{i=1}^n}(\mathbf{w}^Tx_i-y_i)^2+\frac{\lambda}{2}\scriptstyle{\sum_{j=1}^d}\mathbf{w}_j^2 \\ f(\mathbf{w})=\frac{1}{2}||\mathbf{Xw-y}||^2+\frac{\lambda}{2}||\mathbf{w}||^2\]- 앞에 있는 term = 기존 활용하던 Least Square
- 뒤에 있는 term = 특정 w가 커지지 않도록 조절
- Least Square와 동시에 w의 크기값도 함께 줄이려고 노력함
- $\boldsymbol{\to}$ Regularization term
- $\boldsymbol{\lambda}$ = Hyper Parameter
- 람다가 커질수록 w값들의 크기가 더 작아짐
- 람다가 작아질수록 w값들이 커지는 것을 어느정도 허용함
- 람다값은 Validation Set을 통해 최적화
- 학습 데이터 중 일부를 테스트 데이터처럼 다루며 테스트
L2-Regularization and Normal Equations
위 objective function을 vector form으로 표현하면 아래와 같으며,
\[f(\mathbf{w})=\frac{1}{2}||\mathbf{Xw-y}||^2+\frac{\lambda}{2}||\mathbf{w}||^2\]vector form에 대하여 미분을 취하면 아래와 같이 $+\lambda \mathbf{w}$ term이 새롭게 발생하게 되는데,
\[\nabla f(w)=\mathbf{X}^T\mathbf{Xw-X}^T\mathbf{y+}\lambda\mathbf{w}\]위 미분값이 0이 되는 지점의 w = 우리가 구하고자 하는 값
\[(\mathbf{X}^T\mathbf{X}+\lambda\mathbf{I})\mathbf{w}=\mathbf{X}^T\mathbf{y}\]- 기존 Regression Model
- $\mathbf{X}^T\mathbf{X}$가 미분 가능할 때에만 w를 얻을 수 있다
- 미분 불가능할 경우 w를 구하지 못하는 상황이 발생함
- $\mathbf{X}^T\mathbf{X}+\lambda\mathbf{I}\to$ 항상 미분 가능
- 학습 안정성이 매우 높아지는 효과
- regularization term을 추가함으로써 항상 w를 얻을 수 있다
Regularization term 적용은 오버피팅 문제를 해결함과 동시에 학습 안정성도 높일 수 있는 아주 좋은 방법이 됨
Regularization term은 거의 항상 고민되고 고려되고 추구되고 있음을 항상 기억할 것
Other types of regularization
- L1-regularization
- 아웃라이어에 강한 norm
- 미분 불가능 지점이 0일 때 존재
- Huber norm 활용
- L0-norm
- 0이 아닌 것의 갯수를 세는 것
- L0-norm을 regularization으로 쓴다는 것의 의미?
- w값들 중 0이 아닌 것들의 숫자를 최소화하자
- feature dimension을 전반적으로 보는 게 아니라 선택적으로 보게 됨
- feature를 보게 되는 w값들 대부분이 0으로 빠지게 되고, 0으로 된다는 의미는 w에 대응되는 feature를 아예 무시한다는 의미가 됨
- L0-norm은 sparsity norm이라는 다른 이름으로 매우 빈번하게 활용
- 특히 현재 입력되고 있는 feature들 중에서 우리가 특정 결과값을 얻을 때 좀 더 중요한 feature들을 고르고자 할 때 L0-norm을 적극적으로 활용 가능
- 0-1 loss function과 동일하게 모든 영역에서 미분 불가능하고 미분값이 0으로 빠지게 되므로, L0-norm 추정을 위해 sigmoid function 또는 L1-norm을 활용할 수 있다
K-mooc, 딥러닝의 깊이 있는 이해를 위한 머신러닝, 중앙대학교 첨단영상대학원 영상학과 최종원 교수님
*그래프 이미지 출처: 강의자료