선형 모델을 위한 noise-robust 학습 방법론

작성일 | In ,

선형 모델은 Regression과 Classification 문제에 모두 활용되는 중요한 알고리즘입니다. 오늘은 선형 모델이 갖는 근본적인 문제점을 살펴본 뒤, 어떻게 문제점을 보완하고 견고한 모델을 만들 수 있는지 알아봅니다.

*먼저 읽어보면 좋은 글 > Linear Regressor vs. Linear Classifier

알아볼 내용들

  • 데이터에 노이즈가 있으면 어떤 결과가 나올까?
  • 노이즈에 강인한 학습 방법은 무엇이 있을까?
  • RANSAC 알고리즘이란 무엇일까?

데이터의 노이즈가 머신러닝에 미치는 영향 이해하기

노이즈에 강인한 머신러닝 방법론을 학습하고, 실제 환경에 적합한 것을 활용하기

데이터에 노이즈가 있으면 어떤 결과가 나올까?

Least Squares with Outliers

Least Squares는 아웃라이어에 취약한 특성을 지님

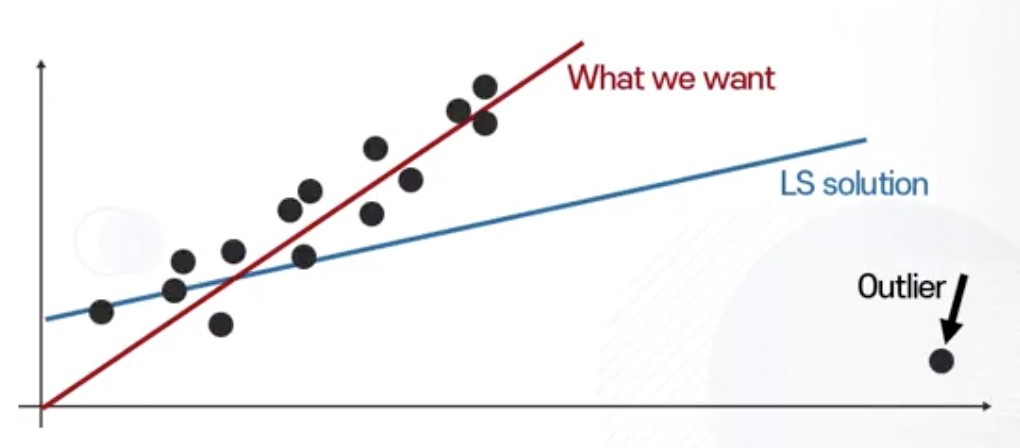
image-20210124200900077

Least Square에서 노이즈에 취약하게 반응하는 이유

에러가 커질수록 Least Squares가 지나치게 크게 증가한다.

  • 에러가 커질수록 Cost가 기하급수적으로 커짐
    • 에러가 작을 때 = 줄일 필요성 적다고 판단
    • 에러가 클 때 = 아주 많이 줄여야 한다고 판단 (큰 에러에서 loss 값이 훨씬 크기 때문)
  • 위 문제를 해결하기 위하여 L1-norm 사용

노이즈에 강인한 학습 방법은 무엇이 있을까?

Robust Regression

에러가 커지더라도 줄여야 하는 loss 값은 똑같은 수식이 주어진다면?

  • 좀 더 에러가 작은 것들의 에러를 줄이기 위해 노력하게 됨
  • 제곱값(squared value) 아닌 절대값(absolute value) 사용
\[f(\mathbf{w}) = \sum_{i=1}^n|\mathbf{w}^T\mathbf{x}_i-y_i|\]
  • 에러 크기와 상관없이 줄여야 하는 loss 값(중요도)이 항상 동일

Assumption: 일반적으로 노이즈의 비율은 전체 inliers보다는 적다

  • 전체 데이터에서 다수 샘플을 정확하게 맞추려고 노력
  • 틀린 값을 가진 적은 갯수의 샘플(outliers)은 무시
    • 그러나 절대값은 활용하기 힘들다

Robust Regression with L1-norm

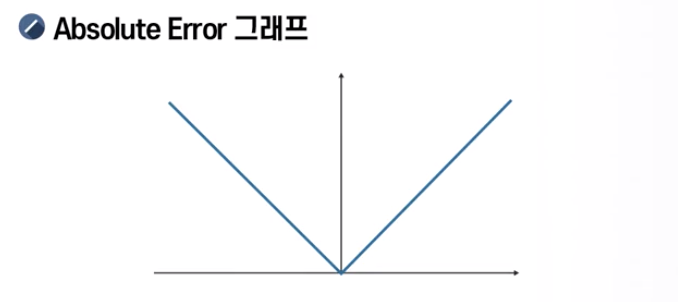
image-20210124201944817

  • loss = 0일 때 미분 불가능 (기울기 정의 불가)
  • 미분을 통한 결과값을 얻는 방법론 적용 불가능
  • Regression 모델에 대부분의 sample loss를 0으로 만들려고 하는 학습 방법을 적용하기 힘들게 됨
    • 이를 추정하여 미분 가능한 함수로 변환해야 함

Huber Loss

Absolute Error와 Least Square의 장단점을 합친 것

  • 특정 $\epsilon$ (epsilon) 보다 작을 때
    • Least Square 적용
    • 장점 = 모든 영역에서 미분 가능
  • 특정 $\epsilon$ (epsilon) 보다 클 때
  • absolute error 적용
  • 장점 = 아웃라이어에 대해 강인함
\[f(w) = \sum_{i=1}^nh(w^x_i-y_i)\] \[h(r_i)= \begin{cases} \frac{1}{2}r_i^2, & \mbox{, for }|r_i|\leqq \epsilon \\ \epsilon(|r_i|-\frac{1}{2}\epsilon), & \mbox{ , otherwise} \end{cases}\]

$h$ for huber loss

  • 모든 포인트에 대해서 미분 가능
  • 에러 크기에 따른 변화량은 항상 일정하게 고정

Infinite Norm Regression

노이즈가 있는 데이터에 관심을 갖는 Regression Model인 경우 활용해야 하는 Error?

  • 에러값의 최대값을 최소화하는 방향으로 loss 설계
\[f(w)=||\mathbf{Xw-y}||_{\infty} \ \text{where }||r||_\infty=\underset{\ \ i}max\{|r_i|\}\]
  • Max가 infinite norm 형태로 표현
    • Infinite norm은 얻어진 모든 샘플 에러 중 가장 큰 값만 출력
  • 최대값을 갖는 것에 대하여 minimize loss
    • 무시하지 않고 오히려 노이즈에 관심을 갖는 새로운 형태의 Regression Modeling 가능
  • Convex 하긴 하지만 미분 불가능 포인트 존재함
    • 노이즈, 아웃라이어에 더 집중적으로 Regression Model을 맞추려는 노력
    • max function to log sum exponential form
    • 0-1 loss function 사례와 유사 (미분가능/계산편리)
\[\underset{\ \ \ i}max\{|z_i|\}\approx log(\scriptstyle\sum_iexp(z_i))\]

노이즈에 관심이 많은 모델도 알아둬야 하는 이유

  • 다양한 머신러닝 환경이나 데이터 특징에 따라서 역으로 노이즈에 관심을 갖는 형태를 활용하는 경우 발생
  • 다양한 기법을 알고 있는 상태에서 현재 주어진 문제 상황과 적용 문제의 머신러닝 기법에 따라 적절한 방법을 택할 수 있어야 함

RANSAC 알고리즘이란 무엇일까?

  • 노이즈가 꽤 많은 비중으로 존재하는 상황에서
  • 아웃라이어의 정보들을 무시해야 할 때 사용

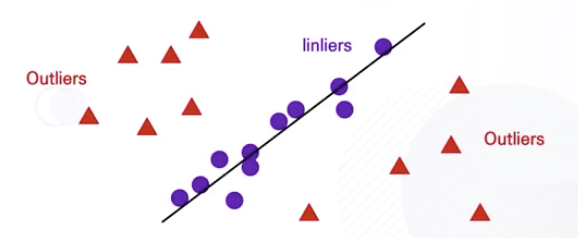
image-20210124205226351

1-norm regression : 아웃라이어에 여전히 영향을 받음

  • 아웃라이어의 값들을 원천적으로 배제하는 방법?
    • 수많은 데이터 샘플 존재할 때 인라이어가 대다수를 차지하는 상황
    • 그 외 아웃라이어들은 Regression Model에 도움되지 않는 상황

RANSAC의 목표

  • 인라이어의 갯수를 최대화하는 Linear Regression Model 탐색
  • 아웃라이어는 아예 최적화 과정에서 고려하지 않도록 배제

RANSAC의 작동 과정

  1. 처음 주어진 학습 데이터 중 일부분만 선택
  2. 선택된 샘플들 만으로 Linear Regression Model 계산
  3. 계산한 Linear Regression Model로 인라이어 및 아웃라이어 구분
  4. 1-3 반복
  5. 가장 많은 인라이어를 갖는 Linear Regression Model 최종 선택
  6. 최종 인라이어들을 활용해서 마지막 Linear Regression Model 계산하면 RANSAC 종료

Assumption to Reasoning

  • (가정) 데이터 중 인라이어가 대다수를 차지할 것이다
  • (추론) 가장 많은 인라이어를 갖는 모델이 좋은 모델일 것이다

image-20210124205818330

RANSAC의 장점

  • Robust Regression
    • 아웃라이어 정확한 탐지 불가
    • 모델 학습 과정에서 아웃라이어까지 고려함
  • RANSAC
    • 대다수 인라이어를 찾으면 아웃라이어는 일괄 삭제
    • 아웃라이어들이 전혀 도움이 되지 않고 무조건 배제되어야 좋은 상황일 경우
      • RANSAC 알고리즘을 통해 좋은 Regression Model을 찾을 수 있음
    • 컴퓨터 비전, 음성 인식, 실제 머신러닝 알고리즘들에서 다양하게 활용되고 있음
    • 아웃라이어들을 삭제하는 필수적인 알고리즘 중 하나로 인식

K-mooc, 딥러닝의 깊이 있는 이해를 위한 머신러닝, 중앙대학교 첨단영상대학원 영상학과 최종원 교수님

*그래프 이미지 출처: 강의자료