Generalization은 Supervised Learning으로 학습한 prediction 함수가 테스트 데이터에 대해서도 일반적으로 잘 작동할 수 있도록 하는 방법입니다. Generalization의 주요한 방법으로서, 이번 포스팅에서는 모델의 언더피팅과 오버피팅을 컨트롤하기 위한 정규화를 살펴봅니다.
Generalization
Bias and variance
- Model bias = 예측값과 실제값 간의 variance
- 예측값이 실제값을 얼마나 잘 맞추고 있는가
- Model variance = 예측 함수의 variation
- 예측모델이 그리는 그래프가 얼마나 변동성이 심한가
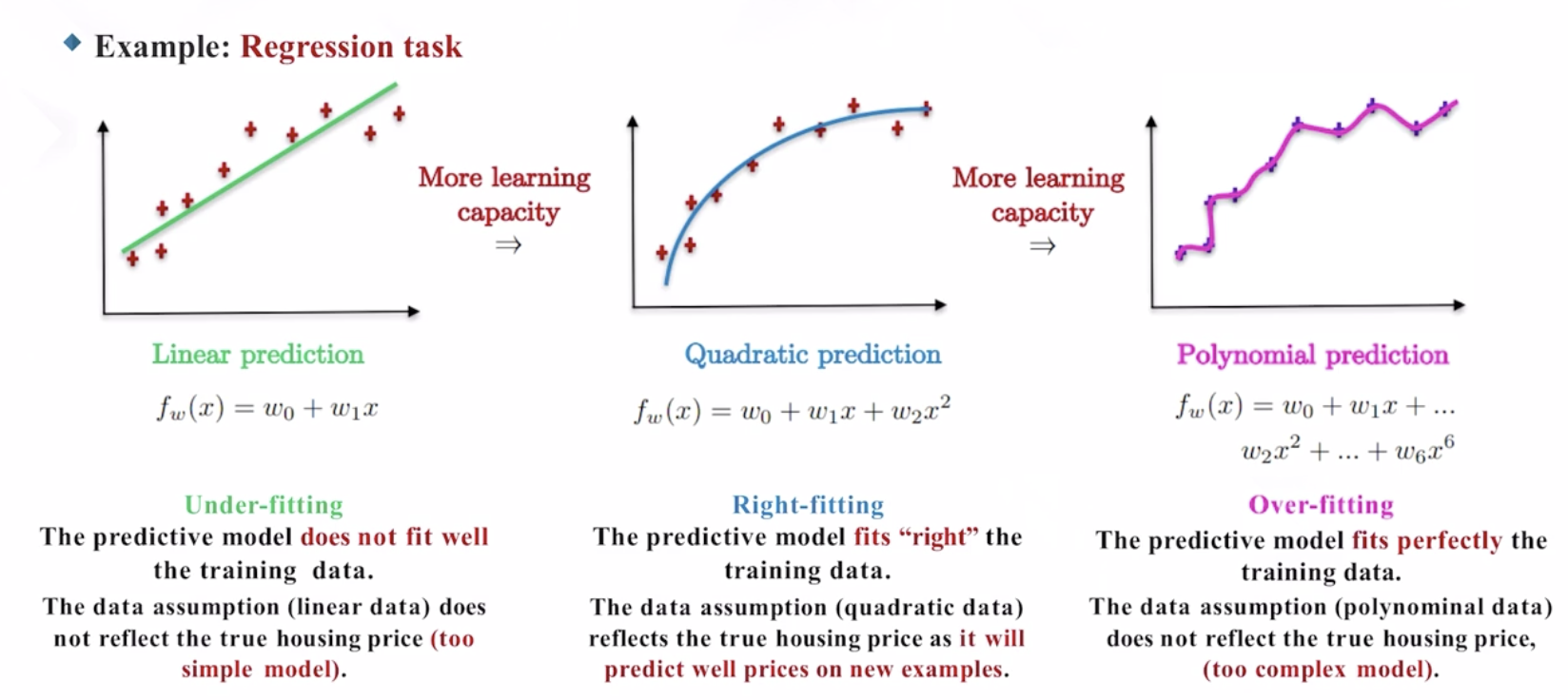
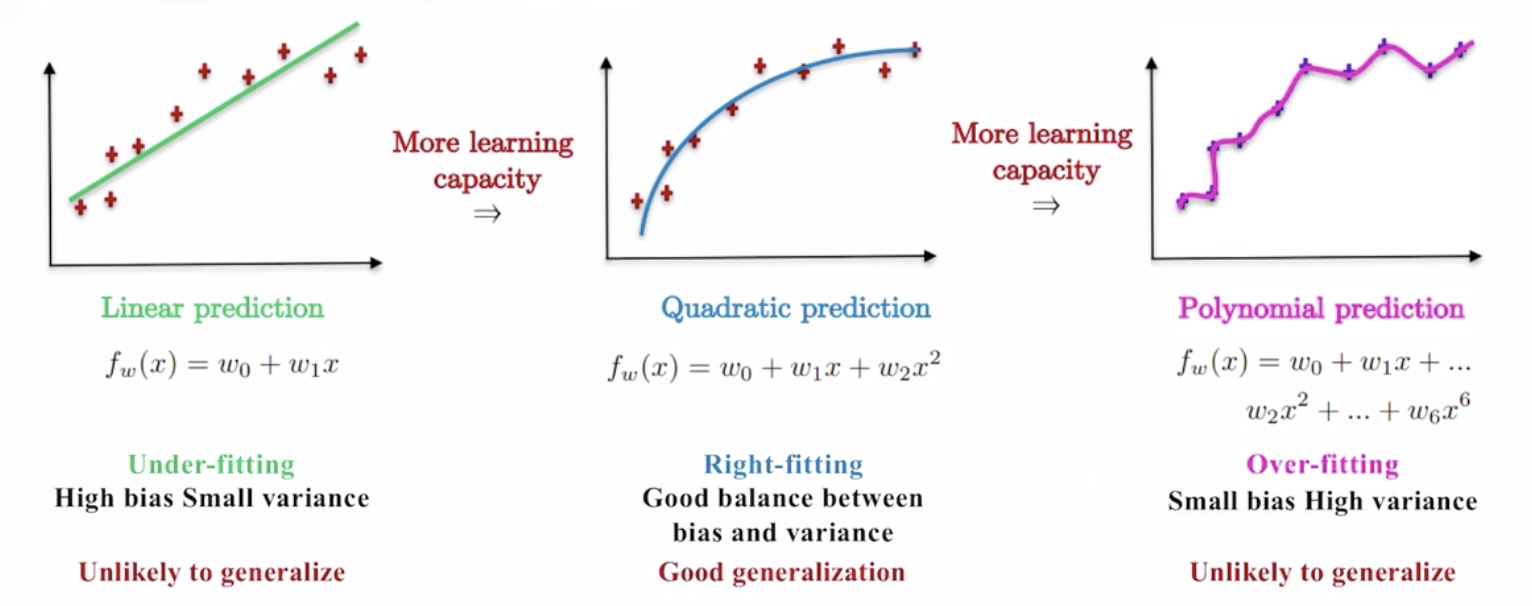
- Under-fitting
- Model bias 높음
- Model variance 낮음
- Not generalized
- Right-fitting
- Model bias - Model variance 균형 상태
- Generalized
- Over-fitting
- Model bias 낮음
- Model variance 높음
- Not generalized
The problem of over-fitting
- 오버피팅(과적합) 문제는 신경망 네트워크 등에서 가장 흔하게 발생
- 예측 모델이 큰 learning capacity를 갖고 있으므로, 트레이닝 데이터에 대해 loss를 매우 작게 최소화할 수 있음
- 특정한 weight parameter에 큰 숫자를 부여하게 됨
- 그러나 전혀 본 적 없는 새로운 테스트 데이터에 대해서는 0에 가깝게 loss를 줄이는 데 실패 »> 오버피팅**
다른 관점에서 바라 본 오버피팅 문제
- 예측 공간이 지나치게 비대함
- 유의미한 예측이 이루어지기 어려움
- 차원의 저주 (curse of dimensionality)
- 데이터가 너무 많은 피쳐를 갖고 있을 때, 매우 높은 차원의 공간에 데이터가 위치하게 되므로 오버피팅 문제는 더 중요해짐
How to address over-fitting?
2 Generalization options to fix the over-fitting issue:
- Feature Reduction (차원축소, 피쳐 줄이기)
- 임의로 피쳐 일부를 배제하거나, 보다 유의미한 피쳐만 선택하는 feature selection 수행
- 단점들:
- 학습 데이터에서는 중요하지 않았지만, 테스트 데이터에서는 중요한 정보를 잃어버릴 수 있음
- Feature selection 모델도 완벽하게 동작하는 것은 아님
- Regularization (정규화)
- 데이터와 해결하고자 하는 문제에 따라 피쳐들의 중요도를 조정
- 장점들:
- 모든 피쳐들의 정보를 보존
- 모델이 학습 단계에서 weight 값들을 고려함
- dimension이 아주 큰 데이터에 효과적
Intuition
Idea
3차함수와 같은 high-capacity 함수로부터 시작하여, weight values $w_3, w_4$를 작아지도록 유도한다.
- high-capacity 함수는 더 단순하고, 더 부드러운 함수(ex. 2차함수)로 변환된다.
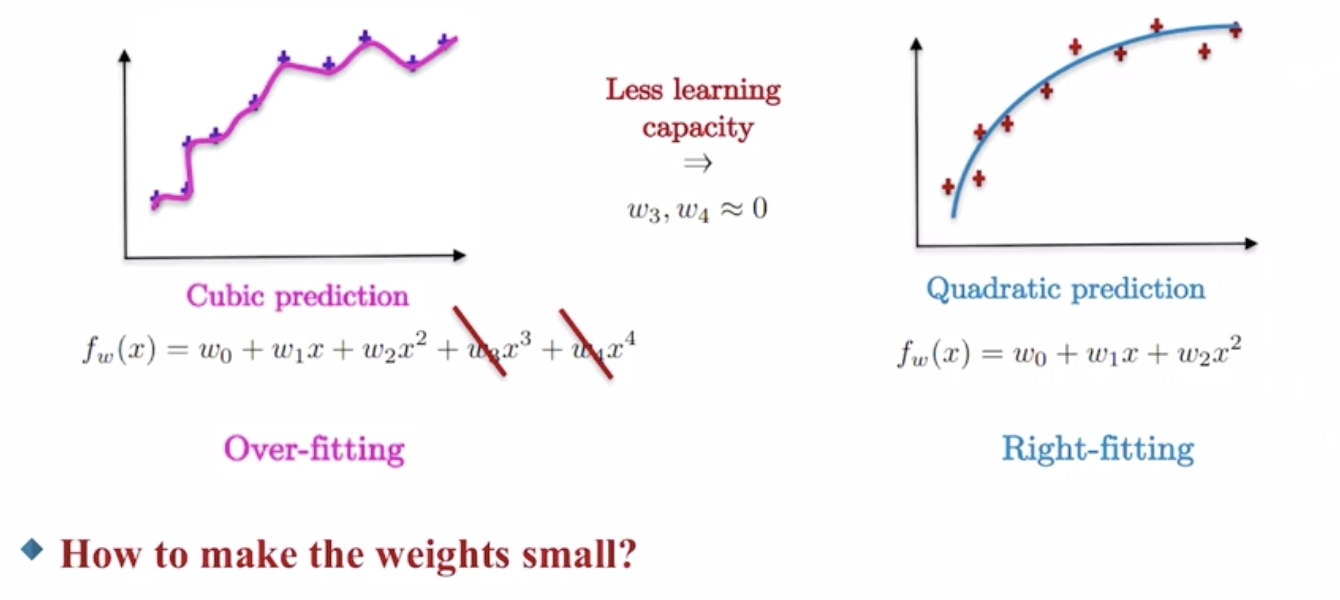
Penalization
가중치의 값이 커지는 것에 페널티를 부여함으로써 가중치를 작아지도록 강제할 수 있다.
\[\underset{ \ \ w} min \frac{1}{n}\sum_{i=1}^n(f_w(x_i)-y_i)^2+1000\cdot w_3^2+1000 \cdot w_4^2\]$w_3, w_4$가 조금이라도 커지면 최소화하고자 하는 값 전체가 급격하게 증가하므로, $w_3, w_4$를 작은 값만 갖도록 강제하는 효과를 발생시킨다.
\[f_w(x) = w_0+w_1x+w_2x^2+w_3x^3+w_4x^4 \ \ \ \underset{w_3, w_4 \approx 0}\implies \ \ \ f_w(x)=w_0+w_1x+w_2x^2\]Regularization
Term and Loss
Idea
- high-capacity 예측함수로 시작하여, 예측함수의 parameter weights 값에 페널티를 부여하는 regularized loss를 최적화함으로써 더 부드러운 형태의 lower-capacity 함수를 학습한다.
Data Fidelity term
\[\frac{1}{n}\sum_{i=1}^n (f_w(x_i)-y_i)^2\]- Fitting loss between predictive function and training data
- 모델과 데이터의 차이를 최소화시킴
Regularization term
\[\frac{\lambda}{d}\sum_{j=1}^dw_j^2\]- Penalty/regularization loss (enfocing small values) a.k.a 1.2 loss
- 예측 함수 자체의 regularity, 즉 variation을 최소화시킴
| Fit | Cause | desired $\boldsymbol\lambda$ |
|---|---|---|
| Over-fitting | 오차 과대평가 (겁쟁이) | increase $\lambda$ |
| Under-fitting | 오차 과소평가 (끓는물 개구리) | decrease $\lambda$ |
Regularized regression loss
\[\underset{\ \ w}min \ L(w)=\frac{1}{n}\sum_{i=1}^n (f_w(x_i)-y_i)^2+\frac{\lambda}{d}\sum_{j=1}^dw_j^2 \\ for \ f_w(x)=w^Tx\]Regularized classification loss
\[L(w)=-\frac{1}{n}\sum_{i=1}^ny_ilog \ p_w(x_i)+(1-y_i)log(1-p_w(x_i))+\frac{\lambda}{d}\sum_{j=1}^dw_j^2 \\ for\ p_w(x) = \sigma(w^Tx)\]Optimization by gradient descent
- Optimization: $\underset{w}min \ L(w)$
- Gradient descent: $w_j \leftarrow w_j-\tau \frac{\partial}{\partial w_j}L(w)$
- Gradient:
Decreasing effect
Gradient descent: \(w_j \leftarrow \tau \frac{\partial}{\partial w_j}L(w) \\ \\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ w_j \leftarrow w_j - (\frac{2\tau\lambda}{d})w_j-\tau \frac{1}{n}\sum_{i=1}^n(y_i-f_w(x_i))x_{i(j)} \\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ w_j \leftarrow (1-\frac{2\tau\lambda}{d})w_j-\tau \frac{1}{n}\sum_{i=1}^n(y_i-f_w(x_i))x_{i(j)}\)
Shrinking effect to $(1-\frac{2\tau\lambda}{d})$
- $ \frac{2 \tau \lambda}{d}$ 는 0에서 1 사이의 값
- Regularization parameter ($\lambda$)
- Learning rate ($\tau$)
- Number of weights ($d$)
- $\lambda, \tau, d$에 따라서 $w_j$가 얼마나 빨리 감소하는지 결정됨
Normal Equation
Solution of MSE loss with linear predictive function:
\[L(w)=\frac{1}{n}(f_w(x_i)-y_i)^2 \\ \big\Downarrow \\ \underset{w}min \ L(w) \Leftrightarrow \frac{\partial}{\partial w} L(w)=0 \Rightarrow w = (X^TX)^{-1}X^Ty \\\]Regularization with normal equation
Regularized regression loss:
\[L(w) = \frac{1}{n}\sum_{i=1}^n(f_w(x_i)-y_i)^2+\frac{\lambda}{d}\sum_{j=1}^dw_j^2\\ \big\Downarrow \ \ \text{Matrix-vector representation} \\ L(w)=\frac{1}{n}(Xw-y)^T(Xw-y)+\frac{\lambda}{d}w^Tw\]Gradient:
\[\frac{\partial}{\partial w} \ L(w)=\frac{\partial}{\partial w}\left[ \frac{1}{n}(Xw-y)^T(Xw-y)-\frac{\lambda}{d}w^Tw \right] \\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ = \frac{1}{n}\frac{\partial}{\partial w} \left[ (w^TX^T-y^T)(Xw-y) \right]+\frac{\lambda}{d}\frac{\partial}{\partial w} \left[w^Tw\right] \\ = \frac{2}{n}X^T(Xw-y)+\frac{2\lambda}{d}w \\ \big\Downarrow \ \ \text{identity matrix} \ Iw=w \\ \ \ \ \ \ \ \ \ = \frac{2}{n}\left( (X^TX+\frac{\lambda}{d}I)w-X^Ty \right) \\ \ \ \ \ \ \ \ \ \ \ \ = 0 \Rightarrow w = (X^TX+\frac{\lambda}{d}I)^{-1}X^Ty\]Normal equation for non-invertible matrix
- Normal Equation은 데이터 차원(피쳐) 갯수보다 샘플 숫자가 적을 경우($n<d$), unique solution을 구할 수 없음
- “over-parametrized linear system of equations”
- 이 경우 행렬 $X^TX$의 역행렬이 존재하지 않음
Examples:
\[a_{11}w_1+a_{12}w_2=b_1 \\ a_{21}w_1+a_{22}w_2=b_2 \\ \text{2 unknowns }w_1, w_2\text{ and 2 equations}\\ \text{"unique solution exists"}\] \[a_{11}w_1+a_{12}w_2=b_1 \\ \text{2 unknowns }w_1, w_2 \\ \text{but 1 equation} \\ \text{infinite number of solutions}\]Solution
- Simply regularize!
K-mooc, 신경망 네트워크와 수학적 기반, 중앙대학교 소프트웨어학부 홍병우 교수님
*그래프 이미지 출처: 강의자료