EM Algorithm
목표
- EM 알고리즘의 핵심적 이론을 이해한다
- 모델의 EM 업데이트를 어떻게 도출하는지 이해한다
Source
Inference with Latent Variables
분류(classification)와 군집화(clustering)는 다르다!
-
가정
-
${X,Z}$ : 가능한 모든 변수들의 집합
-
$X$ : 관측 변수 집합
-
$Z$ : 잠재 변수 집합
-
$\theta$ : 확률분포 모수
- $P(X\vert\theta)=\Sigma_ZP(X,Z\vert\theta)\rightarrow lnP(X\vert\theta)=ln{\Sigma_ZP(X,Z\vert\theta)}$
- 계산식의 문제?
- summation 기호와 로그의 위치가 계산식을 복잡하게 만들고 있음
- 계산식의 문제?
- summation과 로그의 위치를 바꿔주고 싶다!
- Jensen’s Inequality를 사용하자! (다음 항목에서 설명)
-
-
우리가 알고 싶은 것
- $Z,\theta$
- 최적화하고자 하는 계산식 $P(X\vert\theta)=\Sigma_Z P(X,Z\vert\theta)$
- 최적화 과정에서 $Z$와 $\theta$ 는 서로 상호작용함
- $Z,\theta$
Probability Decomposition
$l(\theta)$ for log likelihood given $\theta$ \(l(\theta)=lnP(X|\theta)=ln\{\Sigma_ZP(X,Z|\theta)\}=ln\{\Sigma_Zq(Z)\frac{P(X,Z|\theta)}{q(Z)}\}\)
- Use the Jensen’s ineqaulity
- $\text{ln}{\Sigma_Z q(Z)\frac{P(X,Z\vert\theta)}{q(Z)}}\geq \Sigma_Zq(Z)\text{ln}\frac{P(X,Z\vert\theta)}{q(Z)}$
- Second term? Entropy in information theory!
- $H(X)=-\Sigma_X P(X=x)log_bP(X=x)$
- $Q(\theta,q)=E_{q(Z)}\text{ln}P(X,Z\vert\theta)+H(q)$
- q를 갖는 어떤 분포에 대해서도 참인 명제
- 단, $l(\theta)$ 의 lower bound를 정의할 뿐이라는 아쉬움
- 더 범위를 빠듯하게 좁힐 수 없을까?
- 곡선(실제)과 직선(하한)을 최대한 붙일 수는 없을까?
- 직선(하한)을 최대화시키면 곡선(실제)에 매우 근접하지 않을까?
Jensen’s Inequality?

When $\varphi(x)$ is concave: \(\varphi(\frac{\Sigma a_i x_i}{\Sigma a_j})\geq\frac{\Sigma a_i \varphi(x_i)}{\Sigma a_j}\) When $\varphi(x)$ is convex: \(\varphi(\frac{\Sigma a_i x_i}{\Sigma a_j})\leq\frac{\Sigma a_i \varphi(x_i)}{\Sigma a_j}\)
Concave vs. Convex

$log \ x$ = strictly concave function
- 따라서 로그 함수에 대한 젠슨 부등식의 직선은 로그 함수의 하한선이 된다.
Maximizing the Lower Bound (1)
하한선을 최대화해서 젠슨 부등식 오차를 최소화 시켜보자! \(l(\theta)=\text{ln}P(X|\theta)=\text{ln}\Big\{ \Sigma_Zq(Z)\frac{P(X,Z|\theta)}{q(Z)} \Big\} \\ \geq \Sigma_Zq(Z)\text{ln}\frac{P(X,Z|\theta)}{q(Z)}=Q(\theta,q)\)
-
The other storyline is: \(l(\theta)\geq\Sigma_Z q(Z)\text{ln}\frac{P(X,Z|\theta)}{q(Z)} =\Sigma_Zq(Z)\text{ln}\frac{P(Z|X,\theta)P(X|\theta)}{q(Z)} \\ =\Sigma_Z\{q(Z)\text{ln}\frac{P(Z|X,\theta)}{q(Z)}+q(Z)\text{ln}P(X|\theta)\} \\ =\text{ln}P(X|\theta)+\Sigma_Z\{q(Z)\text{ln}\frac{p(Z|X,\theta)}{q(Z)}\} \\ \\ L(\theta,q)=\text{ln}P(X|\theta)-\Sigma_Z\{q(Z\text{ln}\frac{q(Z)}{P(Z|X,\theta)}\}\)
-
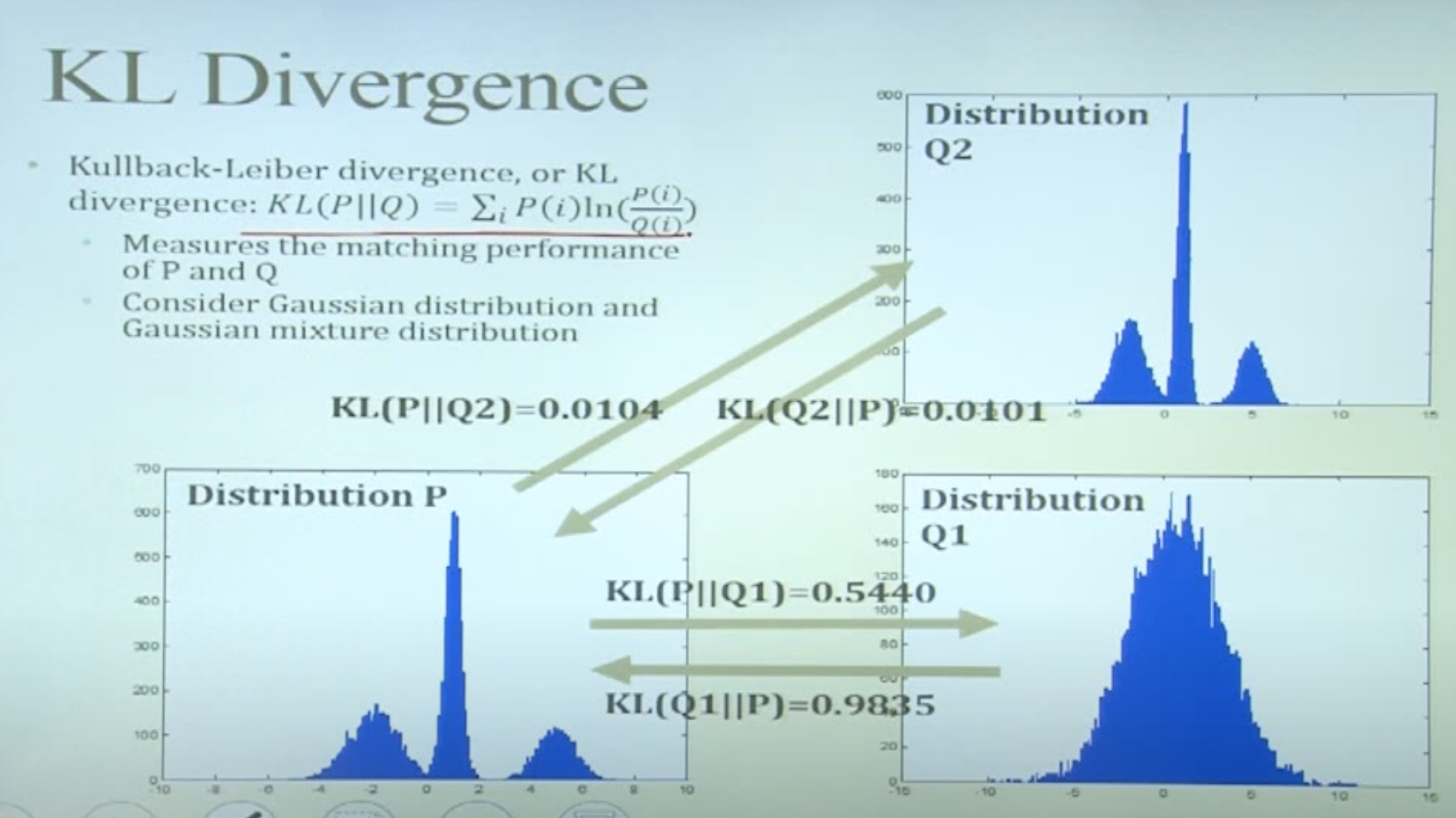
여기서 두번째 항은 매우 특별한 식을 의미함! \(KL(q(Z)\vert\vert P(Z\vert X,\theta))=\Sigma_Z\{q(Z)\text{ln}\frac{q(Z)}{p(Z \vert X,\theta)}\}\)
- 쿨백-라이블러 다이버전스(KL divergence): $KL(P\vert \vert Q)=\sum_iP(i)\text{ln}\frac{P(i)}{Q(i)}$
- 위 계산식은 이산형 분포인 경우 (연속형인 경우 단순합이 아닌 적분을 취하여 계산)
- 서로 다른 두 확률분포의 차이를 계산하는 비대칭 측정법
- $KL(P \vert \vert Q)\geq0$
- 두 분포가 동일하면 $KL(P \vert \vert Q)=0$
- 쿨백 라이블러 발산은 거리 개념이 아니다!
- $KL(P \vert \vert Q)\neq KL(Q \vert \vert P)$
- 선행하는 분포 관점에서 다른 분포와의 차이를 계산하기 때문에 값이 상대적이다
- 정보이론 관점에서 KL 발산을 최소화하는 것은 크로스 엔트로피를 최소화하는 것과 동일하다!
- 쿨백-라이블러 다이버전스(KL divergence): $KL(P\vert \vert Q)=\sum_iP(i)\text{ln}\frac{P(i)}{Q(i)}$
-
Maximizing the Lower Bound (2)
Derivation from the Jensen’s inequality: \(l(\theta)=\text{ln}P(X|\theta)=\text{ln}\Big\{ \Sigma_Zq(Z)\frac{P(X,Z|\theta)}{q(Z)} \Big\}\geq \Sigma_Zq(Z)\text{ln}\frac{P(X,Z|\theta)}{q(Z)}=Q(\theta,q)\)
$Q(\theta,q)$ in the form of the Jensen’s inequality & informational theory: \(Q(\theta,q) = E_{q(Z)}\text{ln}P(X,Z|\theta)+H(q)\)
$L(\theta,q)$ to be maximized for approximating real $l(\theta)$
- Specifically, the second term in $L(\theta,q)$ is to be minimized
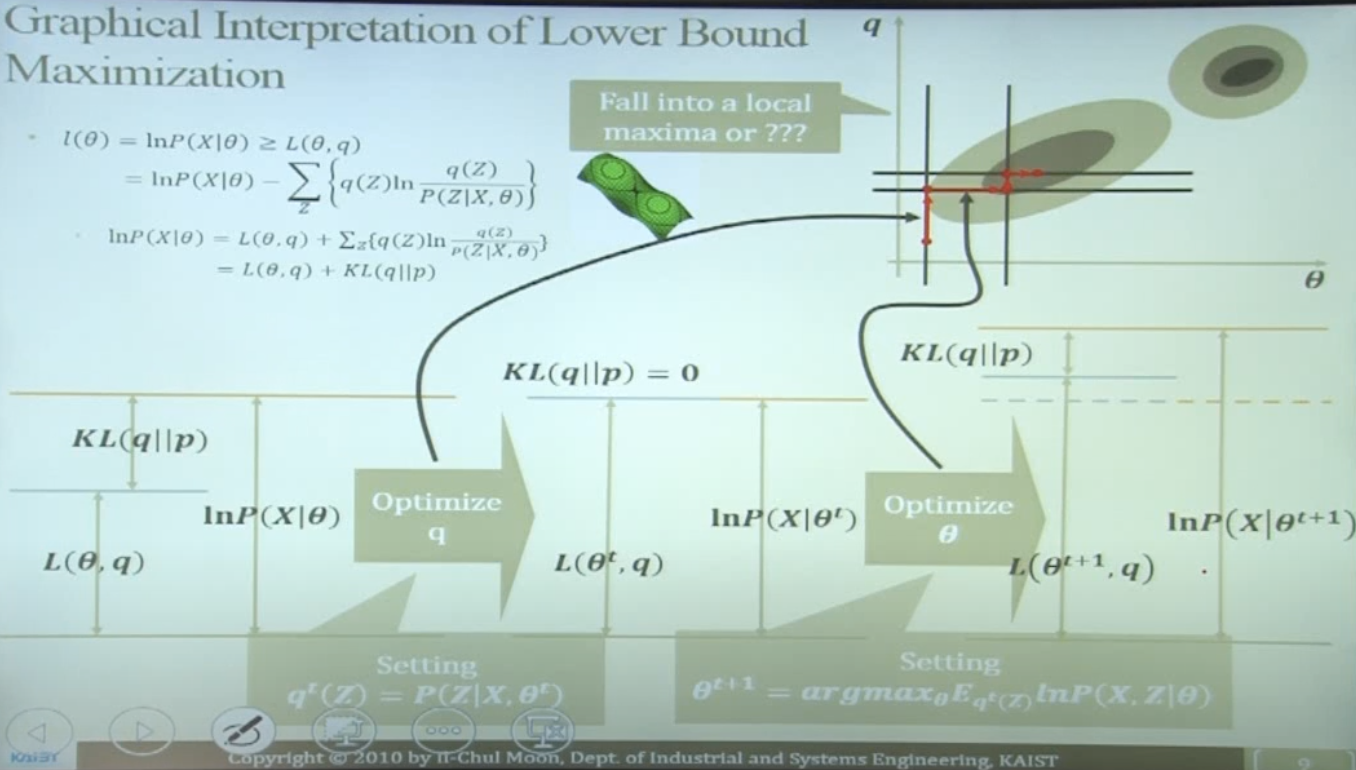
$L(\theta,q)$를 계산해야 하는 이유?
- 우리는 $q(Z)$에 대한 추가적인 지식/정보 없이는 $Q(\theta,q)$를 업데이트할 수 없다
- 업데이트의 의미 = 실제 모수에 더 근사한 값으로 최적화
- $L(\theta,q)$의 두번째 항인 KL Divergence는 $q(Z)$를 어떻게 업데이트 해 나가야 할 지를 알려준다
- $L(\theta,q)$의 첫번째 항은 t 시점에서 고정 (상수)
- $L(\theta,q)$의 두번째 항은 $L(\theta,q)$ 최대화를 위해 최소화될 수 있다
- $KL(q(Z) \vert \vert P(Z \vert X,\theta))=0 \rightarrow q^t(Z)=P(Z \vert X,\theta^t)$
- (정보이론 관점) $q(Z)$와 $P(Z \vert X,\theta)$ 간의 차이가 작아지면 실제 log likelihood에 가깝게 다가갈 수 있다
- 최적화된 $q$에 대한 lower bound는 다음과 같이 업데이트:
- $Q(\theta,q^t)=E_{q^t}\text{ln}P(X,Z \vert \theta^t)+H(q^t)$
- more tight lower bound (=maximized $Q(\theta,q)$)를 얻기 위해 $\theta$ 최적화 진행
- $\theta^{t+1}=argmax_\theta Q(\theta,q^t)=argmax_\theta E_{q^t (Z)}\text{ln}P(X,Z\vert\theta)$
- $q^t(Z) \rightarrow$ t 시점에 계산된 잠재변수의 분포 모수
- $\text{ln}P(X,Z\vert\theta)\rightarrow$ t+1 시점에 업데이트 최적화 된 log likelihood 모수
- $\theta^{t+1}=argmax_\theta Q(\theta,q^t)=argmax_\theta E_{q^t (Z)}\text{ln}P(X,Z\vert\theta)$
한 번에 $l(q)$를 추정할 수는 없지만,
- KL Divergence를 반복적인 업데이트를 통해 최소화시킨다면 진짜 $l(q)$에 근사한 값을 구할 수 있다!
Graphical Interpretation of Lower Bound Maximization
EM Algorithm
- EM Algorithm
- 잠재변수를 포함하는 모델에 대해서 maximum likelihood 해를 찾는 알고리즘
- $P(X\vert\theta)=\Sigma_ZP(x,Z\vert\theta)\rightarrow\text{ln}P(X\vert\theta)=\text{ln}{\Sigma_ZP(X,Z\vert\theta)}$
- EM Process
- $\theta^0$ 임의의 값으로 모수 초기화
- 업데이트되는 Likelihood가 수렴할 때까지 이하 반복 루프
Expectation Step
\[q^{t+1}(z)=argmax_q Q(\theta^t,q)=argmax_q L(\theta^t,q)=argmin KL(q \vert \vert P(Z\vert X,\theta^t)) \\ \rightarrow q^t(z)=P(Z \vert X,\theta)\rightarrow Assign \ Z \ by \ P(Z \vert X,\theta)\]Maximization Step
\[\theta^{t+1}=argmax_\theta Q(\theta,q^{t+1})=argmax_\theta L(\theta, q^{t+1})\]- Z 고정의 의미 = 현재 가진 데이터가 모든 관측 데이터
- 일반적인 Maximum Likelihood Estimation (최대우도추정법, MLE)와 동일한 최적화 방법
Re-thinking GMM Learning Process
- GMM & K-Means
- 잠재변수의 최적 할당과 관련 분포 모수를 찾기 위해서 EM 알고리즘을 사용함
- EM Algorithm in GMM
- $\theta^0$ 임의의 값으로 모수 초기화
- 업데이트되는 Likelihood가 수렴할 때까지 이하 반복 루프
Expectation Step
- Assign Z by $P(Z \vert X,\theta)$
Maximization Step
일반적인 Maximum Likelihood Estimation (최대우도추정법, MLE)와 동일한 최적화 방법 \(\frac{d}{d \mu_k}\text{ln}P(X \vert \pi,\mu,\Sigma)=0, \ \frac{d}{d \Sigma_k}\text{ln}P(X \vert \pi,\mu,\Sigma)=0, \ \frac{d}{d \mu_k}\text{ln}P(X \vert \pi,\mu,\Sigma)+\lambda(\Sigma^K_{k=1}\pi_k-1)=0\)
\[\hat{\mu_k}=\frac{\Sigma^N_{n=1}\gamma(z_{nk})x_n}{\Sigma^N_{n=1}\gamma(z_{nk})}\] \[\Sigma_k=\frac{\Sigma^N_{n=1}\gamma(z_{nk})(x_n-\hat{\mu_k})(x_n-\hat{\mu_k})^T}{\Sigma^N_{n=1}\gamma(z_{nk})}\] \[\pi_k=\frac{\Sigma^N_{n=1}\gamma(z_{nk})}{N}\]