Gaussian Mixture Model and EM Algorithm

목표

다항분포 및 다변수 가우시안 분포를 이해한다
혼합 모델이 왜 유용한지 이해한다
가우시안 혼합 모델로부터 파라미터 업데이트가 어떻게 도출되는지 이해한다

Source

AAILab Kaist 머신러닝 강좌 (K-Means Clustering and Gaussian Mixture Model)
공돌이의 수학정리노트 - 가우시안 혼합 모델 & EM 알고리즘

배경지식: 최대우도법

우도(Likelihood)

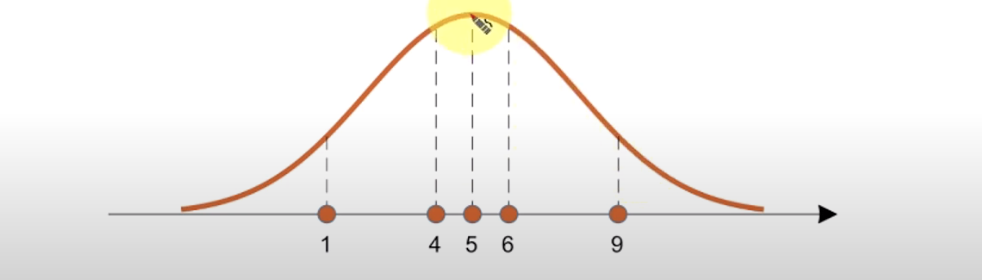
각 데이터 샘플에서 후보 분포에 대응하는 높이(확률)를 다 곱한 값
- “특정한 모수를 갖는 분포가 주어졌을 때, 관측 데이터가 등장할 확률들을 모두 곱한 값”
  - log를 적용할 경우 (log likelihood) 확률곱이 아닌 확률합으로 계산할 수 있음!

\[\prod^m_{t=1}p(x^{(t)}|\theta)\]

최대우도법(Maximum Likelihood Estimation)

어떤 데이터를 관찰하고 데이터에 맞는 모수를 추정하는 방법
가령, 주어진 데이터에 대한 정규분포 fitting
- “어떤 정규분포가 주어진 데이터에 가장 잘 들어맞나?”

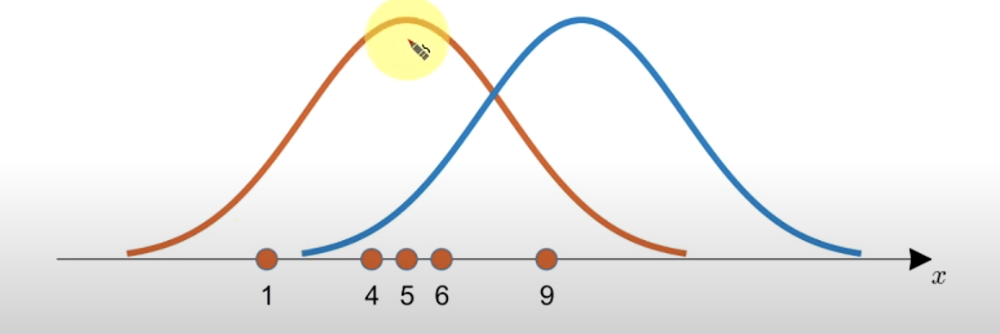
정규분포를 가정했을 때, 우도(likelihood)를 최대화하는 모수는?
- 상세한 식 전개는 생략 (다음 항목에서 순차 설명)

\[\hat{\mu}=\frac{1}{m}\sum^m_{t=1}x^{(t)}\] \[\hat{\sigma}^2=\frac{1}{m}\sum^m_{t=1}(x^{(t)}-\hat{\mu})^2\]

Multinomial Distribution

가우시안 혼합 모델을 이해하기 위해서는 먼저 다항분포를 알아야 한다.

Binary variable
0도또는 1을 선택한다 -> 이항분포 (binomial distribution)
K개의 선택지가 존재한다면?
- X=(0,0,1,0,0,0) when K=6 and selecting the third option
- \[\sum_k x_k =1, \ P(X|\mu)=\prod^K_{k=1}\mu_k^{x_k} \ such \ that \ \mu_k \geq 0, \ \sum_k \mu_k=1\]
  - $x_k$ : k번째 위치의 값 (0 or 1)
  - $\mu_k$ : 전체에서 k번째 위치의 값을 선택할 확률
- 이항분포를 일반화하여 표현하면 -> 다항분포 (Multinomial distribution)
Given a dataset $D$ with $N$ selections, $x_1, …,x_n$
- $\mu$가 주어졌을 때 X가 관측될 확률?
- $P(X\vert\mu)=\prod^N_{n=1}\prod^K_{k=1}\mu_k^{x_nk}=\prod^K_{k=1}\mu_k^{\sum^N_{n=1}x_{nk}}=\prod^K_{k=1}\mu_k^{m_k}$
  - When $m_k=\sum^N_{n=1}x_{nk}$
  - N개의 선택지 중에 $k$ 번째 옵션을 선택한 갯수
- $\mu$ 의 maximum likelihood 해를 어떻게 결정할 수 있을까?
  - MLE(Maximum Likelihood Estimation) = 주어진 파라미터에서 어떤 선택지가 나올 확률을 최대화시켜주기
    - Maximize $P(X\vert\mu)=\prod^K_{k=1}\mu_k^{m_k} \ when \ m_k=\sum^N_{n=1}x_{nk}$
    - 제약조건: $\mu_k \geq 0, \ \sum_k \mu_k=1$

Lagrange Method

라그랑주 메소드 = 제약조건 하에서 local maximum을 찾는 방법
- Target to maximize : $f(x,y)$
- Constraint : $g(x,y)=c$
- $f, g$가 실수 편미분을 갖는다고 가정
  1. 라그랑주 function & multiplier
    
    기본형 $L(x,y,\lambda)=f(x,y)+\lambda(g(x,y)-c)$
    
    $L(\mu, m, \lambda)=\sum^K_{k=1}m_k$ln$\mu_k +\lambda(\sum^K_{k=1}\mu_k-1)$
    - Using the log likelihood (additional treatment)
  2. 1차 편미분을 취한 값을 0으로 set:
    
    $\frac{d}{d\mu_k}L(\mu,m,\lambda)=\frac{m_k}{\mu_k}+\lambda=0 \rightarrow \mu_k=-\frac{m_k}{\lambda}$

최적값을 구하기 위해 제약조건 활용 $\sum_k \mu_k = 1 \rightarrow \sum_k - \frac{m_k}{\lambda}=1\rightarrow\sum_km_k=\lambda\rightarrow\sum_k\sum^N_{n=1}x_{nk}=\lambda\rightarrow N=-\lambda$
- $N$ for number of selectable options ($x_1, x_2, …,x_n$)
  - $\mu_k=\frac{m_k}{N}$ : MLE parameter of multinomial distribution

Multivariate Gaussian Distribution

가우시안 분포의 확률밀도함수(probability density function)

$N(x\vert\mu,\sigma^2)=\frac{1}{\sqrt{2\pi\sigma^2}}exp(-\frac{1}{2\sigma^2}(x-\mu)^2)$
$N(x\vert\mu,\Sigma)=\frac{1}{(2\pi)^{D/2}} \frac{1}{\vert\Sigma\vert^{1/2}}exp(-\frac{1}{2}(x-\mu)^T \Sigma^{-1}(x-\mu))$
- $\text{ln} N(x\vert\mu,\Sigma)=-\frac{1}{2}\text{ln} \ \vert\Sigma\vert-\frac{1}{2}(x-\mu)^T \Sigma^{-1}(x-\mu)+C$
- $\text{ln} \ N(x\vert\mu,\Sigma)=-\frac{N}{2}ln \ \vert\Sigma\vert-\frac{1}{2}\sum^{N}_{n=1}(x_n-\mu)^T \Sigma^{-1}(x_n-\mu)+C$
  - $\propto-\frac{N}{2}\text{ln}\vert\Sigma\vert-\frac{1}{2}\sum^N_{n=1}Tr[\Sigma^{-1}(x_n-\mu)(x_n-\mu)^T]$
  - $=-\frac{N}{2}\text{ln}\vert\Sigma\vert-\frac{1}{2}Tr[\Sigma^{-1}\sum^N_{n=1}((x_n-\mu)(x_n-\mu)^T)]$
- \[\frac{d}{d_\mu}\text{ln}N(X\vert\mu,\Sigma)=0\rightarrow -\frac{1}{2}\cdot2\cdot-1\cdot\Sigma^{-1}\sum^N_{n=1}(x_n-\hat{\mu})=0\rightarrow\hat{\mu}=\frac{\sum^N_{n=1}x_n}{N}\]
- \[\frac{d}{d\Sigma^{-1}}lnN(X|\mu, \Sigma)=0\rightarrow\hat{\Sigma}=\frac{1}{N}\sum^N_{n=1}(x_n-\hat{\mu})(x_n-\hat{\mu})^T\]
  - 식 전개방식은 다소 복잡함 (자세한 설명은 생략)
  - “Trace Trick”을 사용한 다음, 아래 특성을 활용
  - $\frac{d}{dA}log\vert A\vert=A^{-T}$
  - $\frac{d}{dA}Tr\vert AB\vert=\frac{d}{dA}Tr\vert BA\vert=B^T$

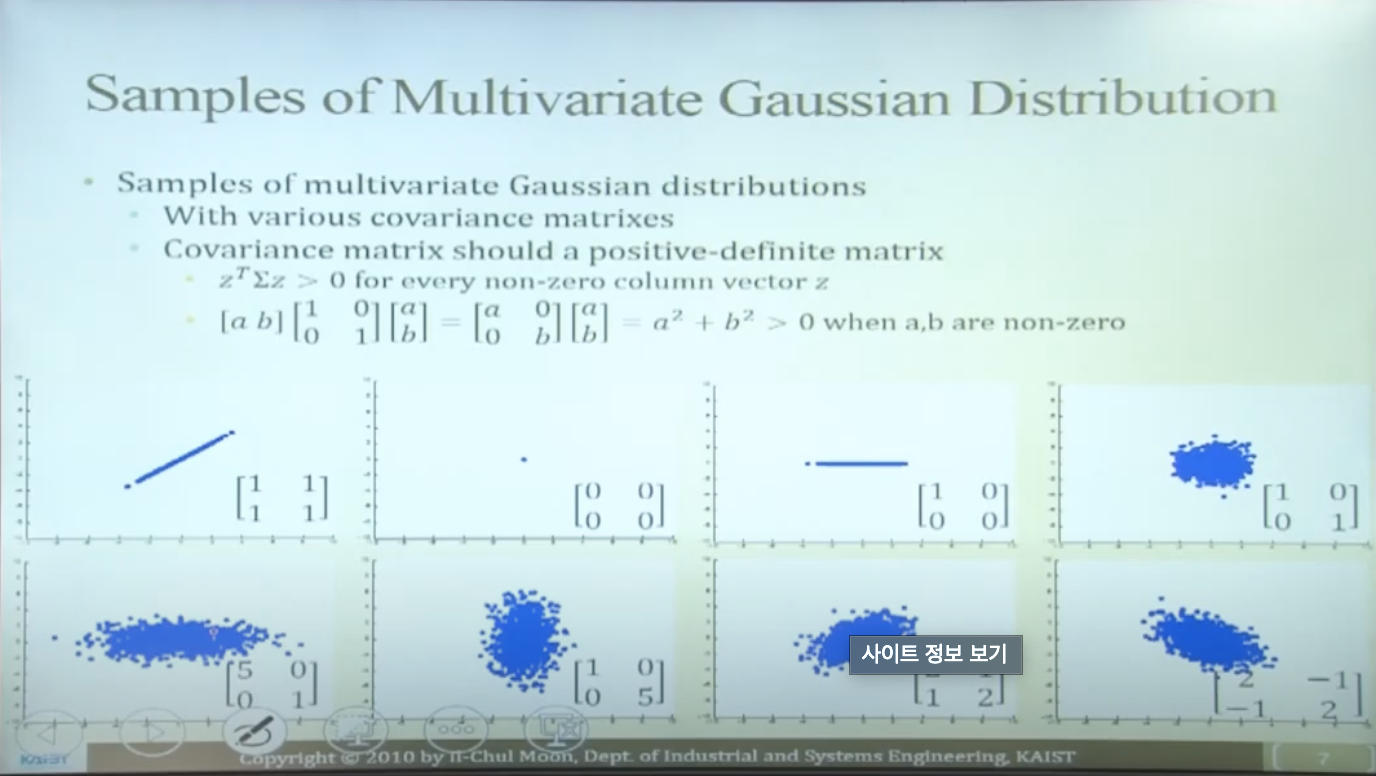
Samples of Multivariate Gaussian Distribution

다양한 공분산 매트릭스를 갖는 다변수 가우시안 분포 샘플

공분산 매트릭스는 n차원 공간에서의 샘플 데이터 형태를 설명

Mixture Model

서로 다른 3개의 정규분포에서 뽑은 샘플들이 (동일한 공간에) 존재한다고 가정하자
- Subpopulation (아집단, 부분 모집단)
- 전통적인 (단일) 분포 모델로는 우리가 가정한 분포를 정확하게 설명할 수 없음
- 세 개의 정규분포를 혼합(mix)할 필요가 있음
  - 샘플에 적합한 새로운 분포를 생성해야 한다
  - =혼합 모델(Mixture Distribution)
$P(x)=\Sigma^K_{k=1}\pi_k N(x\vert\mu_k,\sigma_k)$
- 혼합계수(mixing coefficients) $\mu_k$: 확률적으로 K개의 옵션으로부터 하나의 정규분포를 선택
  - 일종의 가중치(weight)로서 작용
  - $\Sigma^K_{k=1}\pi_k=1, \ 0\leq\pi_k\leq1$
    - 0과 1 사이, 모두 합하면 1 = 가중치이면서 확률이기도 함!
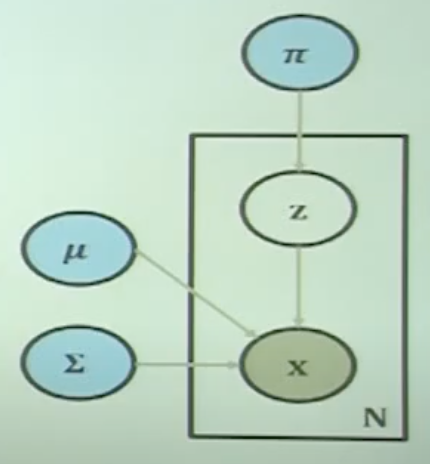
  - 이러한 확률/가중치로부터 뽑은 분포는 어떤 분포인가?
    - 개별 분포에 대응하는 변수 Z를 새롭게 introduce
- 혼합요소(mixture component) $N(x\vert\mu_k, \sigma_k)$ : subpopulation에 대한 개별 분포
$P(x)=\Sigma^K_{k=1}P(z_k)P(x\vert z)$
- $K$개의 분포에서 하나를 뽑은 뒤, 데이터 $x$ 가 해당 분포로부터 sampling 되었을 확률들의 합
- Why this ordering of variables?

Gaussian Mixture Model

관측 데이터가 여러 개의 다변수 가우시안 분포들로 구성된 혼합 분포로부터 샘플링 되었다고 가정해 보자!

$P(x)=\sum^{k}_{k=1}P(z_k)P(x|z)=\sum^K_{k=1}\pi_kN(x|\mu_k,\Sigma_k)$

이러한 혼합 분포를 어떻게 모델링할까?
- Mixing Coefficient or Selection Variable $z_k$
  - 선택(selection)은 다항분포를 따르는 확률적 과정 (stochastic process)
  - $z_k\in{0,1}, \ \Sigma_kz_k=1, \ P(z_k=1)=\pi_k, \ \Sigma^K_{k=1}\pi_k=1, \ 0\leq\pi_k\leq1$
- Mixture Component
  - $P(X\vert z_k=1)=N(x\vert \mu_k,\Sigma_k)\rightarrow P(X \vert Z)=\prod^K_{k=1}N(x \vert\pi_k, \Sigma_k)^{\pi_k}$
조건부확률 관점에서 계산?
- $\gamma(z_{nk})=p(z_k=1 \vert x_n)=\frac{P(z_k=1)P(X \vert Z_k=1)}{\Sigma^k_{j=1}P(z_j=1)P(x \vert z_j=1)}$
- $=\frac{\pi_kN(x \vert \mu_k,\Sigma_k)}{\Sigma^K_{j=1}\pi_jN(x \vert \mu_j,\Sigma_j)}$
전체 데이터셋에 대한 log likelihood
- $lnP(X\vert\pi,\mu,\Sigma)=\Sigma^N_{n=1}\text{ln}{\Sigma^K_{k=1}\mu_kN(x\vert\mu_k,\Sigma_k)}$

Expectation of Gaussian Mixture Model

K-Means 알고리즘과 유사한 문제
- 두 개의 모수(parameter)가 서로 상호작용하고 있음 (닭이 먼저냐 달걀이 먼저냐)
- K-Means와 유사하게 EM 알고리즘을 적용할 수 있음
  - Expectation Step: 개별 데이터 포인트를 클러스터에 할당
  - Maximization Step: 모수 업데이트

Expectation Step

관측 데이터 각각을 가장 가까운 클러스터에 할당하기 = 할당 확률을 따름
- 클러스터 = 확률분포 (soft clustering)
- 클러스터 할당 확률 = likelihood given the parameters and the data point
\[\gamma(z_{nk})=p(z_k=1 \vert x_n)=\frac{P(z_k=1)P(X \vert Z_k=1)}{\Sigma^k_{j=1}P(z_j=1)P(x \vert z_j=1)}=\frac{\pi_kN(x \vert \mu_k,\Sigma_k)}{\Sigma^K_{j=1}\pi_jN(x \vert \mu_j,\Sigma_j)}\]
- $x, \pi,\mu,\Sigma$ 주어진 상태에서 $\gamma(z_{nk})$ 를 계산
- $\gamma(z_{nk})$ 는 $\pi,\mu,\Sigma$ 계산에 사용됨
- $\gamma(z_{nk})$ 가 새롭게 업데이트되면 기존 파라미터 또한 업데이트되어야 함

Maximization of Gaussian Mixture Model

Maximization Step

Expectation 계산 결과인 $\gamma(z_{nk})$ 가 주어진 상황에서 파라미터 $\pi,\mu,\Sigma$ 업데이트
- \[\text{ln}P(X\vert\pi,\mu,\Sigma)=\sum^N_{n=1}ln\{\Sigma^K_{k=1}\pi_kN(x\vert\mu_k,\Sigma_k)\}\]
- Typical update methods
  - 미분
    - 함수가 연속형일 때 미분식 = 0으로 놓고 계산
  - 라그랑주 메소드
    - 파라미터에 제한조건이 존재할 경우

Derivative Method

\[\frac{d}{d\mu_k}lnP(X\vert\pi,\mu,\Sigma)=0\]

\[\frac{d}{d\mu_k}lnP(X\vert\pi,\mu,\Sigma)=\Sigma^N_{n=1}\frac{\pi_kN(x\vert\mu_k,\Sigma_k)}{\Sigma^K_{j=1}\pi_jN(x\vert \mu_j,\Sigma_j)}\Sigma^{-1}(x_n-\hat{\mu_k})=0 \\ \rightarrow\sum^N_{n=1}\gamma(z_{nk})(x_n-\hat{\mu_k})=0 \\ \rightarrow\hat{\mu_k}=\frac{\Sigma^N_{n=1}\gamma(z_{nk})x_n}{\Sigma^N_{n=1}\gamma(z_{nk})}\]

\[\\ \frac{d}{d\Sigma_k}\text{ln}P(X\vert \pi,\mu,\Sigma)=0\]

\[\rightarrow\Sigma_k=\frac{\Sigma^N_{n=1}\gamma(z_{nk})(x_n-\hat{\mu_k})(x_n-\hat{\mu_k})^T}{\Sigma^N_{n=1}\gamma(z_{nk})}\]

Lagrange method applied

\[\frac{d}{d\pi_k}\text{ln}P(X\vert\pi,\mu,\Sigma)+\lambda(\Sigma^K_{k=1}\pi_k-1)=0\]

\[\rightarrow \sum^N_{n=1}\frac{N(x\vert\mu_k,\Sigma_k)}{\Sigma^K_{j=1}\pi_jN(x\vert\mu_j,\Sigma_j)}+\lambda=0 \rightarrow \sum^K_{k=1}\Big\{ \sum^N_{n=1} \frac{\pi_kN(x\vert\mu_k,\Sigma_k)}{\Sigma^K_{j=1}\pi_jN(x\vert\mu_j,\Sigma_j)}+\pi_k\lambda \Big\}=0\]
\[\rightarrow\lambda=-N\rightarrow\pi_k=\frac{\Sigma^N_{n=1}\gamma(z_{nk})}{N}\]

EM Progress of Gaussian Mixture Model

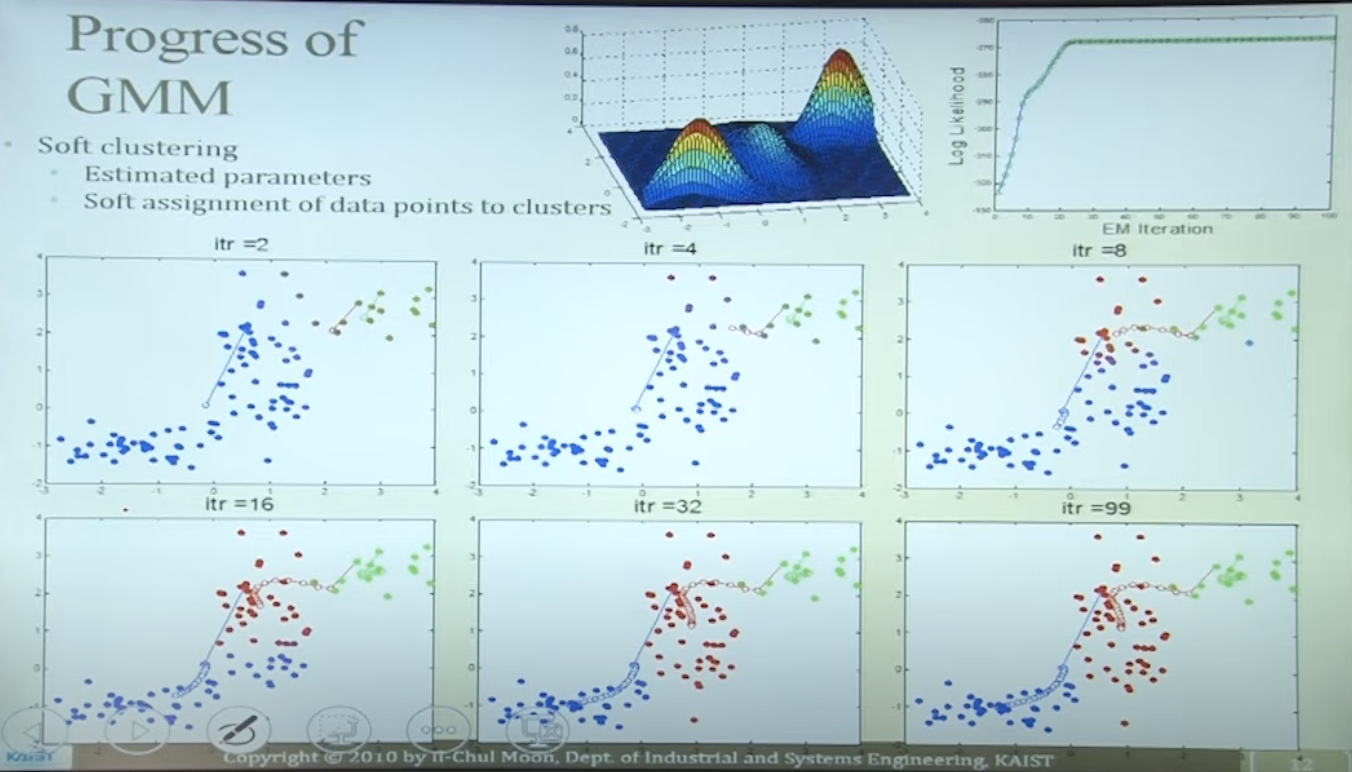
Properties of Gaussian Mixture Model

Pros and Cons

Pros
- More information
  - Soft clustering
  - Not a simple and discrete assignment
    - Information loss
- More and more information
  - Learn the latent distribution
  - Distance is not always the answer of the distribution
Cons
- Long computation time
- Falling into local maximum
- Deciding K