K 평균 클러스터링 알고리즘

작성일

K-Means Clustering Algorithm

목표

  • 비지도학습 이해하기
  • K-평균 iterative process 이해하기
  • K-평균 알고리즘의 한계 이해하기

K-Means 알고리즘 as 비지도학습

  • 실제 값을 모르고, 실제 값이 포함된 트레이닝 셋을 갖고 있지 않을 때 사용
    • 관측 데이터의 발생에는 잠재 팩터(=내부적인 동력)가 작용하고 있으며, 잠재 팩터의 작용으로 인하여 데이터가 복수의 군집으로 나뉜다고 가정한다
  • 사용 목적
    • 데이터 클러스터 찾기
    • 잠재 팩터 찾기
    • 그래프 구조 찾기
  • 사용 예시
    • 문자열 데이터로부터 대표성을 갖는 주제어 찾기
    • 얼굴 이미지로부터 잠재 이미지 요소 찾기
    • 제품 리뷰 점수 데이터의 결측값 완성하기
    • 궤적 데이터(trajectory data)로부터 노이즈 제거하기
  • 방법론
    • 클러스터링
      • 데이터 집합과 데이터 집합에 대한 인스턴스 후보군을 평가하기
    • 필터링
      • 신호와 소음이 혼재하는 데이터로부터 기저 / 주요 신호를 평가하기

Clustering Problem

  • 레이블이 없는 데이터를 어떻게 군집화할까?
    • 클래스에 대한 명확한 사전지식이 없는 상태
    • 클래스에 대한 잠재(latent, hidden) 변수를 가정
    • 관측 데이터 포인트를 각 잠재 클래스에 최적 할당하는 것이 목표
  • 전제
    • 각 클러스터는 동일한 기제 / 내부 동력 / 잠재 팩터를 공유하고 있다
  • 까다로운 문제?
    • 두 개의 클러스터의 경계에 위치하는 애매한 데이터 포인트들에 대한 판단

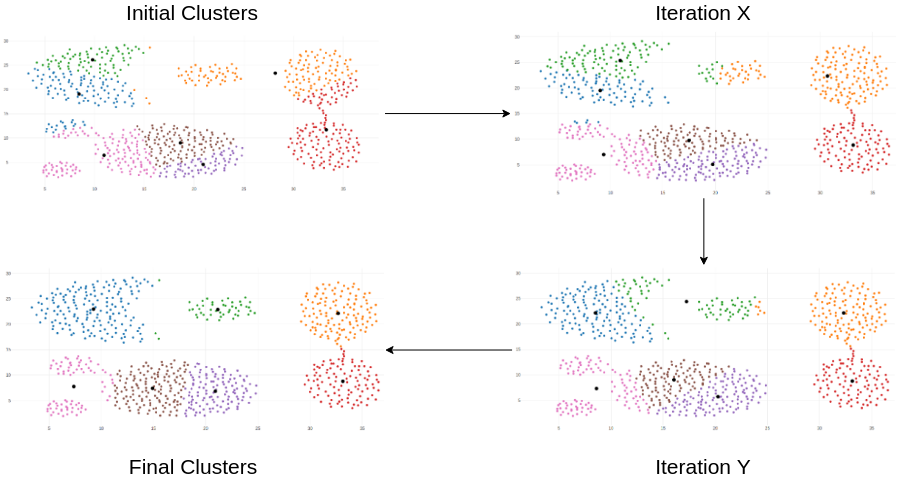
K-Means Iterative Process

  • K-Means Algorithm
    • 관측 데이터 전체에 K개의 잠재 팩터가 작용하고 있다고 가정
    • K개의 잠재 팩터가 작용함으로써 K개의 클러스터가 발생
    • 각 클러스터의 중심점(centroid)으로부터의 거리 기반으로 개별 관측 데이터가 어느 클러스터인지 판단 및 할당
  • 알고리즘 연산식
    • \[J=\sum^{N}_{n=1}\sum^{K}_{k=1}r_{nk}||x_n-\mu_k||^2\]
      • 유클리디안 거리 기반, 각 클러스터 중심점과 클러스터에 속한 데이터 간의 거리의 합
      • 추정해야 하는 파라미터는 2개!
        • $r_{nk}, \ \mu_k$
    • 최적화 연산을 통해 J 함수(거리합)를 최소화
      • $r_{nk} \in {0, 1}$
        • $n$번째 관측 데이터가 $k$ 번째 클러스터에 할당되었는지 여부 (할당=1, 비할당=0)
      • $\mu_k$
        • $k$ 번째 클러스터의 중심점(centroid) 위치값
    • Iterative Optimization
      • 하나가 아닌 두 개의 변수를 최적화해야 함
      • 두 개의 변수는 서로 상호작용하는 관계
      • 반복적인 최적화 과정을 통해 두 개의 변수를 반복 업데이트한다

K-Means vs. K-Nearest Neighbor

  • K-Means
    • 각 데이터 포인트가 어느 클러스터에 포함되어 있는지 모르는 상태
    • k개의 latent factor를 가정하고 iterative optimization 진행
  • K-Nearest Neighbor
    • 각 데이터 포인트가 어느 클러스터에 포함되어 있는지 알고 있는 상태
    • 기준 데이터 포인트에 이웃하는 K개의 이웃 데이터 포인트를 기반으로 클러스터 클래스를 판단
      • ex. K=6개의 이웃을 보았을 때, 4개가 “빨강”이고 2개가 “파랑”이면 “빨강” 클러스터에 속한다고 판단

Expectation and Maximization

잠재변수에 대해서 iterative optimization(expectation step, maximization step)을 진행하여 목적함수를 최소화시키는 알고리즘

  • 목적함수

    • \[J=\sum^{N}_{n=1}\sum^{K}_{k=1}r_{nk}||x_n-\mu_k||^2\]
    • Expectation Step
      • 주어진 파라미터에 의해 계산되는 log-likelihood의 기댓값 구하기
      • (K-Means) 가장 가까운 클러스터 중심점 $\mu_{k}$ 에 대해 관측 데이터 포인트를 할당하는 과정 = $r_{nk}$ 업데이트 (최적화)
      • 첫번째 이터레이션에서는 무작위로 정한 임의의 $\mu_{k}$ 를 사용하여 $r_{nk}$를 업데이트하게 됨
    • Maximization Step
      • 주어진 파라미터로 계산한 log-likelihood의 관점에서 파라미터를 최대화
      • (K-Means) 관측 데이터 포인트의 할당 업데이트 결과 $r_{nk}$ 로부터 다시 클러스터 중심점 위치를 업데이트하기 = $\mu_k$ 업데이트 (최적화)

  • $r_{nk}$

    • $r_{nk}\in{0,1}$
    • $n$번째 데이터 포인트가 $k$번째 클러스터에 할당되었는가(1) 아닌가(0)를 표현하는 discrete variable
      • "이 데이터는 어디에 포함되는 데이터일 것이다"
    • Logical choice : 데이터 포인트 $x_n$에 대해 가장 가까운 클러스터 중심점 $\mu_k$
      • Euclidean Distance 기반 판단

  • $\mu_k$

    • 목적함수 J를 $\mu_k$에 대해 미분

      \[\frac{dJ}{d\mu_k}=\frac{d}{d\mu_k}\sum^{N}_{n=1}\sum^{K}_{k=1}r_{nk}||x_n-\mu_k||^2=\frac{d}{d\mu_k}\sum^{N}_{n=1}r_{nk}||x_n-\mu_k||^2 \\ \\ = \sum^{N}_{n=1}-2r_{nk}(x_n-\mu_k)=-2(-\sum^{N}_{n=1}r_{nk}\mu_k+\sum^{N}_{n=1}r_{nk}x_n)=0\] \[\mu_k=\frac{\sum^{N}_{n=1}r_{nk}x_n}{\sum^N_{n=1}r_{nk}}\]
      • 클러스터에 assign 된 데이터 포인트 집합의 단순 평균 위치값으로 $\mu_k$ 를 업데이트
      • 최초 임의값으로 정의된 $\mu_k$ 를 새롭게 업데이트하고, 이를 기반으로 다음 iteration에서 $r_{nk}$ 를 새롭게 업데이트

Properties of K-Means Algorithm

  • 진짜 클러스터 갯수가 불명확하다 (=잠재 팩터가 실제로 몇 개인지 알 수 없다)
    • K-Means 알고리즘 자체는 클러스터 갯수를 확인할 수 없음
    • Bayesian Non-Parametric 방법론으로 K값 추정 가능 (advanced)
  • 클러스터 중심점 위치의 최초값 (initial location)
    • 일반적으로 중심점 위치값은 사전지식을 활용하거나, 임의로 초기값을 정의함
    • 초기값이 잘못 할당되면 local maxima로 수렴될 위험성 존재함
  • Limitation of distance metric (Euclidean)
    • 유클리디언 거리는 정보가 매우 제한된 상태일 때 사용 (사전지식 없는 상황)
      • 모든 dimension이 동일한 가중치를 갖고 있다고 가정한 계산법
      • 유클리디언 거리를 적용하게 되면 클러스터는 일반적으로 원형으로 형성
    • 그러나 사전지식/ 도메인 지식을 적용할 시, 실제로는 dimension에 따른 가중치가 반영되어야 함
      • 특정 dimension에 가중치를 부여하여 타원형으로 만들어지는 것이 바람직하다면?
  • Hard clustering
    • 데이터 포인트의 할당 여부는 $r_{nk}\in{0,1}$ 로 discrete하게 정의됨
    • 그러나 클러스터 간 경계에 위치한 데이터 포인트를 확률로서 판단해야 할 경우도 존재함
      • ex. A 클러스터에 속할 확률 40%, B 클러스터에 속할 확률 60%
    • Gaussian Mixture Model
      • 각 dimension에 대해 서로 다른 가중치 부여 가능
      • Soft clustering 가능

K-Means Clustering Algorithm Implementation

https://github.com/karankharecha/Big_Data_Algorithms/blob/master/src/k_means_clustering.py

k-means-clustering-implementation

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
import pandas as pd
import numpy as np
import plotly.offline as plt
import plotly.graph_objs as go

pd.set_option('display.max_columns', 10)

def k_means_clustering(path, k):
    data = pd.read_csv(path)
    data = data[['V1', 'V2']]
    
    # 원본 데이터를 비복원 k sampling -> 현재 평균값을 저장함
    k_means = (data.sample(k, replace=False))
    k_means2 = pd.DataFrame() # 이전 평균값 저장할 변수
    clusters = pd.DataFrame() # 클러스터별 거리값 저장할 변수
    
    print('Initial means:\n', k_means)

    # 파라미터 업데이트 전후가 동일하면 수렴으로 판단
    while not k_means2.equals(k_means):
				
        ##########################
      	#### Expectation Step ####
        ##########################
        
        # distance matrix
        cluster_count = 0
        for idx, k_mean in k_means.iterrows():
            # 현재 데이터(k_means)와 이전 데이터(k_means2) 간 유클리디언 거리합 계산 -> clusters에 저장
            clusters[cluster_count] = (data[k_means.columns] - np.array(k_mean)).pow(2).sum(1).pow(0.5)
            cluster_count += 1

        # 현재 데이터 포인트들의 클러스터 할당값 업데이트 (=r_nk)
        # 중심점이 가장 가까운 클러스터를 할당함 (idxmin)
        data['MDCluster'] = clusters.idxmin(axis=1)

        # 현재 데이터(k_means)를 이전 데이터(k_means2)에 저장
        k_means2 = k_means
        
        ###########################
        #### Maximization Step ####
        ###########################
        
        # 현재 데이터(k_means)의 centroid 업데이트 (=mu_k)
        k_means = pd.DataFrame()
        k_means_frame = data.groupby('MDCluster').agg(np.mean)

        k_means[k_means_frame.columns] = k_means_frame[k_means_frame.columns]

        print(k_means.equals(k_means2))

    # plotting
    print('Plotting...')
    data_graph = [go.Scatter(
        x=data['V1'],
        y=data['V2'].where(data['MDCluster'] == c),
        mode='markers',
        name='Cluster: ' + str(c)
    ) for c in range(k)]

    data_graph.append(
        go.Scatter(
            x=k_means['V1'],
            y=k_means['V2'],
            mode='markers',
            marker=dict(
                size=10,
                color='#000000',
            ),
            name='Centroids of Clusters'
        )
    )

    plt.plot(data_graph, filename='../output_files/cluster.html')

    
if __name__ == '__main__':
	k_means_clustering(path='../datasets/k_means_clustering_test_1.csv', k=7)

Source

Kaist AAILab 머신러닝 강좌

K-Means Algorithm Implementation by Karan Kharecha